不確定性原理と真空偏極

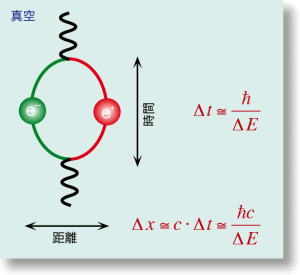
不確定性原理によれば、非常に短い時間であればエネルギーの不確定性はいくらでも大きくなる。

もし時間が寿分短く

ならば、力の粒子は他の粒子・反粒子対に化けることができる。こうして生まれた粒子・反粒子の対は真空偏極と呼ばれる。

真空偏極で生じた粒子、反粒子は、不確定線原理が許す極めて短い時間だけしか存在できないため（すぐに返さなくてはならないエネルギーのごく短期間の借金のようなもの）、仮想粒子と呼ばれる。

仮想粒子は直接観測することはできないが、消えてしまう前に外から十分なエネルギーを注入することができれば、実粒子として観測することができる。

重い粒子の真空偏極ほど、できるのにより大きなエネルギーの不確定性が必要となるので、より短い時間に集中してエネルギーを注入しなくてはならず、一方、光速を超える運動はできないので、これはより小さな領域にエネルギーを集中させなければならないことを意味している。

リニアコライダー実験のような衝突型加速器実験では、粒子衝突によって時空の一点にエネルギーを集中させることで、宇宙創成直後の超高エネルギー状態でしか存在し得なかったような重い粒子を真空から取り出す。

衝突のエネルギーを上げていくと、より短い時間、より短い距離で起こることが見えてくる。