相互作用のバーテックス

基本的な力（もっと一般的に言って相互作用）は、基本粒子が別の基本粒子を放出したり吸収したりすることで起きる。時にはその過程で粒子の種類が変わってしまうこともある。
このような相互作用の様子を表す便利な方法がファイマン図だ（ファイマンは、朝永博士、シュウィンガー博士とともに量子電磁力学を打ち立てた功績でノーベル賞を受賞したアメリカの有名な物理学者）。

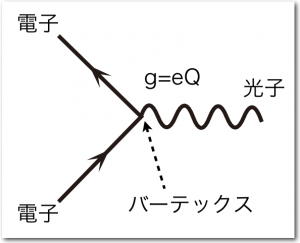
ファイマン図では、基本粒子は線で表される。大雑把に言って、線は基本粒子が運動する際の軌跡だと思っておけばよい。複数の線が一点で交わる所は、それぞれの線で表される基本粒子がそこで相互作用することを意味する。

この相互作用の起こる点のことをバーテックスと呼ぶ。

右の図に電子と光子のバーテックスの例を示した。通常、物質粒子（クォークとレプトン）は普通の実線で表し、力の粒子は波線や螺旋などで表す。光子は波線で表すのが習慣だ。

前のページで説明したように、力の強さは力の粒子のお手玉の頻度できまる。このお手玉の頻度を表す量がバーッテックスの部分に書いた”g”である。

g：大　↔　相互作用が強い

電子と光子の相互作用の場合、g=eQ である。
ここで、”e” は素電荷、つまり陽子の電荷（1.6 x 10^-19 [C]）で、また、Q は素電荷を単位にした時の電荷、電子の場合は Q=-1 であり、u クォークの場合は Q=+2/3、d クォークの場合は Q=-1/3、ニュートリノは Q=0 だ。
電磁気力の強さの目安は電荷の単位 “e” で決まる。
力の種類毎に決まるこのようなチャージの単位を結合定数と呼ぶ。

見かけの力の強さと力の粒子の質量

力の粒子の質量を M とすると、一般に M が小さいほどお手玉は遠くまで届く。
M=0 ならば、お手玉は無限に遠くまで届き遠距離力となる。
逆に M が大きいとお手玉は遠くまで届かず力の及ぶ範囲は狭い範囲に限られて近距離力となる。
つまり、力の本質的な強さは結合の強さを表す “g” で決まるが、力の見かけの強さは力の粒子の質量にもよるのだ。

力の本質的強さは g で決まるが、見かけの強さは M にもよる！

 

力とは力の粒子のやり取り（＝力の粒子の交換）であること、力の本質的な強さは対応するチャージで決まること、力の見かけの強さは力の粒子の質量にもよること、これらを踏まえて自然界の四つの力の話に戻ろう。