Impact parameter resolution ![]() is calculated as
is calculated as
| (105) |
![[*]](foot_motif.gif) .
The effect of external coordinate information can also be
implemented as explained there.
.
The effect of external coordinate information can also be
implemented as explained there.
Let us consider again a tracking device having
(n+1) equally sapced sampling points with an idential spatial
resolution ![]() .For simplicity, we further assume that multiple scattering in
the tracking volume is negligible.
Then the error matrix is given by Eq.B.7, where
the pivot is located at y0 = 0 which is the -th hit position.
When the -th hit is at r = Rin, we need to transform
the error matrix by
.For simplicity, we further assume that multiple scattering in
the tracking volume is negligible.
Then the error matrix is given by Eq.B.7, where
the pivot is located at y0 = 0 which is the -th hit position.
When the -th hit is at r = Rin, we need to transform
the error matrix by ![]() , using
Eq.3.2.19.
Ignoring the material between the -th hit and the interaction point
(by setting ES = 0), we obtain Fig.3.2 which
plots
, using
Eq.3.2.19.
Ignoring the material between the -th hit and the interaction point
(by setting ES = 0), we obtain Fig.3.2 which
plots ![]() as a function of
the ratio of the extrapolation length and the lever arm length:
Rin/(Rout-Rin).
as a function of
the ratio of the extrapolation length and the lever arm length:
Rin/(Rout-Rin).
Notice that the impact parameter resolution here is much worse
in general than that expected from a straight-line approximation.
This is because of the curvature error.
If we have an external tracking device which provides
additional curvature information, we can thus improve
the impact parameter resolution significantly.
We can do this by modifiying ![]() , according to
, according to
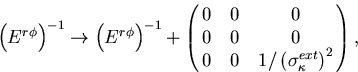 |
(106) |