- ...particles.
-
The vectors in Fig.2.1 are defined by
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
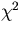
- The terms containing the second derivatives
of
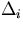 's are proportional to
's are proportional to 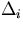 and are hence small and
usually negligible near the
and are hence small and
usually negligible near the 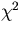 minimum.
minimum.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...space
-
This assumption is valid for a thin material.
If it is not, we can always slice the material into thin enough sublayers and
apply the method explained here repeatedly.
For a high momentum track, a different treatment is possible as
described later.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...material
-
We assume that the fluctuation of the energy loss
is negligible in what follows.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...process
- Notice that the helix parameter
vector so obtained is the one for the original track before energy loss and
multiple scattering, which can then be used for vertexing.
It should be also noted that the track segments combined here may
belong to detector regions with different magnetic fields, as long
as the fields can be regarded as constant in each region.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...linking
- Since any straight line can be
regarded as the zero field limit of some helix,
the results shown below is a special case of the results in the
last subsection
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...follows
- The *'s in
Eq.2.5.34 represent
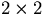 matrices.
matrices.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...HREF="node11.html#EQtrackav">2.5.31
- It is easy to generalize the results to
the cases in which two or more regions of no magnetic field are present.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...by
-
In Subection 2.4.c, we have Taylor-expand
Eq.2.1.1 to the lowest order to get a straight line track.
The track model here, on the other hand, corresponds to
the next order approximation.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...0
-
This does not spoil the generality of our treatment, since
a nonzero
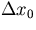 can always recovered as a simple
shift in
can always recovered as a simple
shift in 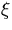 .
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
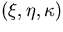
-
We will ignore the small effects on
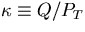 due to the change in the dip angle
due to the change in the dip angle 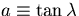 :
which approximation is justifiable when
:
which approximation is justifiable when 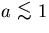 .
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...equation
-
In practice K is usually region-dependent.
We should, therefore, integrate this equation segment by segment.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...HREF="node21.html#EQdematerial">3.2.12
-
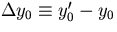 is now a finite shift of the y
coordinate of the pivot.
is now a finite shift of the y
coordinate of the pivot.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...(K=0)
-
In fact, we have
while we know
from Eq.3.2.8.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...sum
-
If the new pivot is within the sensitive volume of the tracker which
measured the track in question, we should drop the ES term,
since the multiple scattering effects
in the tracker must presumably be included
in the original error matrix.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...equation
-
The functional form of
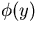 is unknown so that it must be
integrated out eventually.
is unknown so that it must be
integrated out eventually.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...shown
-
Notice that,
in the high momentum limit where the track can be approximated
by a parabola, EM is determined solely by the configuration
of the tracking detector in question:
the y-locations of sampling points
and the spatial resolutions thereat.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...here
- Exact formulae for
EM which are valid for any n are given in Appendix B.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...instead
- This method is applicable also to
thin-layer multiple scattering.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
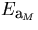
-
As a matter of fact, whether the
particle track is measured before or after the multiple scattering
does not make any difference in the result.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...scattering
-
The multiple scattering only changes
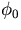 ,
,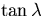 , and, through the change in
, and, through the change in 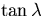 ,
,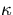 :
:
| 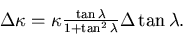 |
(2) |
Notice that the independent variables here are thus  and
and
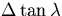 , E'MS in the above expression is diagonal
when we use
, E'MS in the above expression is diagonal
when we use 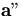 which is
which is 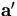 with its
with its 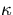 component
set equal to that of
component
set equal to that of 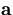 .
This implies that the components of E'MS-1 corresponding to
all but
.
This implies that the components of E'MS-1 corresponding to
all but 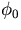 and
and 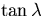 are infinity or in other words
those of E'MS are zero.
Although E'MS-1 is ill-defined in this sense, we can treat
the infinite components as if they are
finite no matter how large and at the end of
calculations let them go to infinity.
are infinity or in other words
those of E'MS are zero.
Although E'MS-1 is ill-defined in this sense, we can treat
the infinite components as if they are
finite no matter how large and at the end of
calculations let them go to infinity.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...y-locations
-
In our coordinate system, y corresponds to r.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
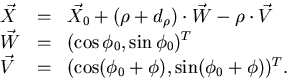
![\begin{displaymath}
\begin{array}
{lll}
\nonumber
\frac{d}{dy_0} E_G
& = & \l...
...ft( \frac{dA}{dy_0} \right) \cdot A^{-1} \right]^T ,\end{array}\end{displaymath}](img138.gif)