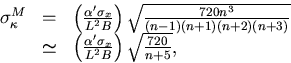Next: About this document ...
Up: No Title
Previous: Effects of Thin Layer
As shown in Section 3, in the high momentum limit,
the r-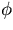 and the r-z track fittings are decoupled so that the
error matrix or its inverse corresponding to
the coordinate measurement errors has a
blockwise diagonal form:
and the r-z track fittings are decoupled so that the
error matrix or its inverse corresponding to
the coordinate measurement errors has a
blockwise diagonal form:
| 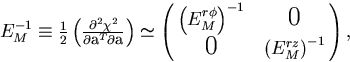 |
(1) |
where the component matrices are given by
| 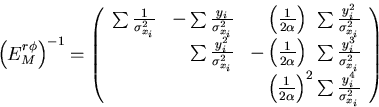 |
(2) |
and
| 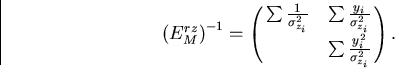 |
(3) |
Notice that, in this limit, the error matrix is determined completely by
the y-locations![[*]](foot_motif.gif) of the sampling points and the spatial resolutions
thereat.
of the sampling points and the spatial resolutions
thereat.
If (n+1) sampling points are equally spaced and have common
resolutions, 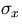 and
and 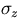 , then the above equations
become
, then the above equations
become
| 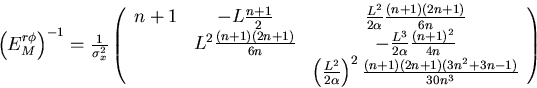 |
(4) |
and
| 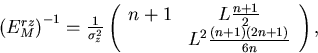 |
(5) |
where we have defined the lever arm length L by
| 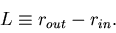 |
(6) |
Notice that in the above equations, we have shown only upper triangles of
the matrices, since they are all symmetric.
By matrix inversions, we thus obtain
| 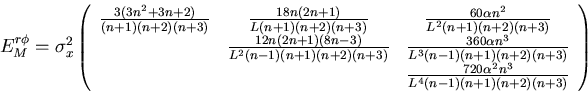 |
(7) |
and
| 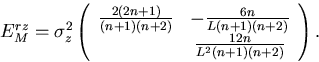 |
(8) |
The above error matrices are defined with the pivotal
point (x0,y0,z0) chosen to be at the -th hit.
From the above formulae, we can estimate, for instance,
the transverse momentum resolution or 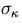 as
as
| 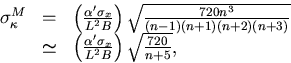 |
(9) |
where the last line is none other thatn the familiar
text book expression
for the momentum resolution valid in the large n limit.



Next: About this document ...
Up: No Title
Previous: Effects of Thin Layer
Keisuke Fujii
12/4/1998
![]() and the r-z track fittings are decoupled so that the
error matrix or its inverse corresponding to
the coordinate measurement errors has a
blockwise diagonal form:
and the r-z track fittings are decoupled so that the
error matrix or its inverse corresponding to
the coordinate measurement errors has a
blockwise diagonal form:
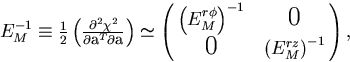
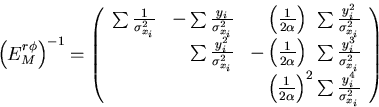
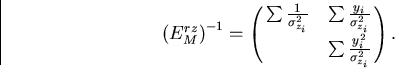
![[*]](foot_motif.gif) of the sampling points and the spatial resolutions
thereat.
of the sampling points and the spatial resolutions
thereat.
![]() and
and ![]() , then the above equations
become
, then the above equations
become
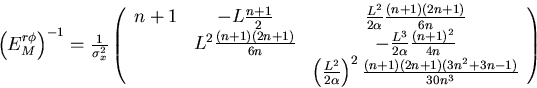
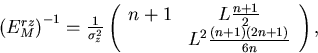
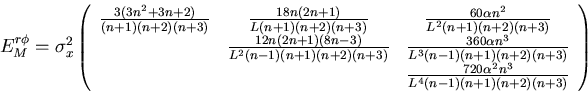
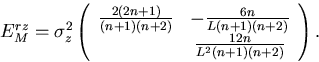
![]() as
as