

Next: Energy Loss Correction
Up: General Discussions without Momentum
Previous: Change of Pivot
In this section, we will show how to extrapolate a helical track through a
material to the other detector region where the magnetic field is not
necessarily present.
For simplicity, we assume that the energy loss and the multiple scattering in
the material take place at a single point in space![[*]](foot_motif.gif) :
: 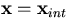 .The track extrapolation is easiest when this interaction point
is chosen as the pivot:
In what follows, it shoud be understood that the track parameters and error
matrrix are pre-transformed to this pivot,
according to the procedure explained in the
last section, unless otherwise stated.
.The track extrapolation is easiest when this interaction point
is chosen as the pivot:
In what follows, it shoud be understood that the track parameters and error
matrrix are pre-transformed to this pivot,
according to the procedure explained in the
last section, unless otherwise stated.
Keisuke Fujii
12/4/1998
![[*]](foot_motif.gif) :
: