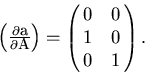Next: Track Fitting under the
Up: Track Fitting in r-
Previous: Pivot Transformation in Vacuum
When the pivot is taken at the point of multiple scattering,
only 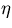 is affected among the track parameters
is affected among the track parameters
![[*]](foot_motif.gif) .
The scattering angle in the r-
.
The scattering angle in the r-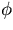 plane
plane
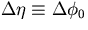 has a variance
has a variance
| 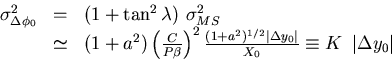 |
(47) |
with 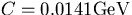 , P and
, P and 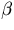 are the
momentum and the velocity of the particle, and X0 is
the radiation length of the material.
This modifies (E)22 and Eq.3.2.9 now becomes
are the
momentum and the velocity of the particle, and X0 is
the radiation length of the material.
This modifies (E)22 and Eq.3.2.9 now becomes
| 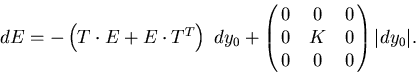 |
(48) |
Notice that 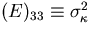 is
not affected by the pivot transformation, which allows
us to readily integrate the above equation
is
not affected by the pivot transformation, which allows
us to readily integrate the above equation![[*]](foot_motif.gif) .
The solution of the above equation can be written in the form:
where EG is the general solution for K = 0, while
ES is a special solution of Eq.3.2.12.
It is easily verified that
.
The solution of the above equation can be written in the form:
where EG is the general solution for K = 0, while
ES is a special solution of Eq.3.2.12.
It is easily verified that
| 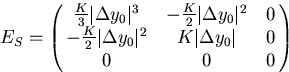 |
(49) |
satisfies Eq.3.2.12![[*]](foot_motif.gif) .
It is also easy to show that
.
It is also easy to show that
| 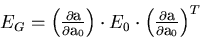 |
(50) |
with
| 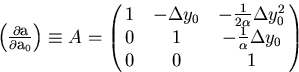 |
(51) |
is the general solution of the homogeneous equation (K=0)![[*]](foot_motif.gif) .
.
In summary, the propagated error matrix at the point which is outside
the area of coordinate measurements is the sum![[*]](foot_motif.gif) :
:
| 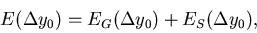 |
(52) |
where EG is the propagated error matrix without taking
multiple scattering into account (Eqs.3.2.15 and 3.2.16)
and ES is the contribution from multiple scattering
(Eq.3.2.14).
Now that we have established the machinary to move the pivot
to anywhere in the detector system, it is easy to implement
the information from external tracking devices.
Assume that we have an extra coordinate measurement
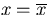 at
at 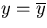 .
Then we take
.
Then we take 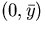 as our new pivot and
minimize
as our new pivot and
minimize
| 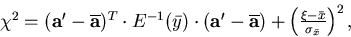 |
(53) |
which is a simple matrix inversion.
The corresponding error matrix can also be readily obtained from
| 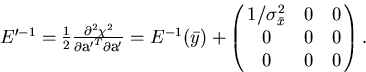 |
(54) |
If there are more than one extra measurements, we can
retransform E' to the next and do the same.
If 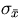 is negligibly small, we might even
include this as a constraint on the track parameter.
In this case, the track becomes
is negligibly small, we might even
include this as a constraint on the track parameter.
In this case, the track becomes
| 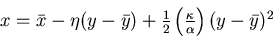 |
(55) |
which has only two parameters:
The error matrix for 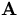 is given by
is given by
| ![\begin{displaymath}
\begin{array}
{lll}
E_{\bf A}
= \left[ \left(\frac{\parti...
...tial {\bf a}}{\partial {\bf A}}\right)
\right]^{-1}\end{array}\end{displaymath}](img149.gif) |
(56) |
with
| 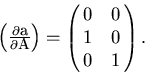 |
(57) |



Next: Track Fitting under the
Up: Track Fitting in r-
Previous: Pivot Transformation in Vacuum
Keisuke Fujii
12/4/1998
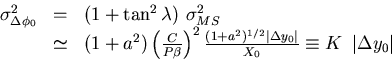
![[*]](foot_motif.gif) .
The scattering angle in the r-
.
The scattering angle in the r-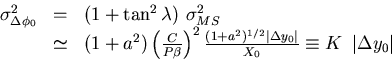
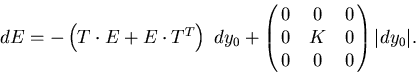
![[*]](foot_motif.gif) .
The solution of the above equation can be written in the form:
.
The solution of the above equation can be written in the form:
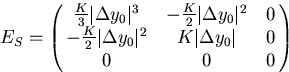
![[*]](foot_motif.gif) .
It is also easy to show that
.
It is also easy to show that
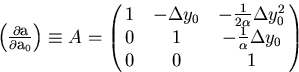
![[*]](foot_motif.gif) .
.
![[*]](foot_motif.gif) :
:
![]() at
at ![]() .
Then we take
.
Then we take ![]() as our new pivot and
minimize
as our new pivot and
minimize
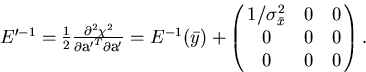
![]() is negligibly small, we might even
include this as a constraint on the track parameter.
In this case, the track becomes
is negligibly small, we might even
include this as a constraint on the track parameter.
In this case, the track becomes