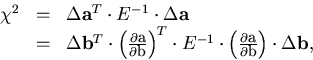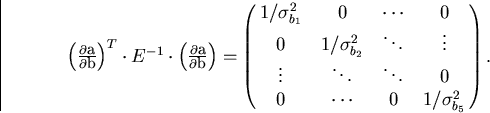

Next: Summary
Up: Examples of Applications
Previous: Impact Parameter Resolution
The full error matrix given by Eqs.3.2.48
and 3.3.77
allows us to smear the exact track parameter given by an
event generator,
properly taking into account the effects of multiple scattering
including the additional correlations among the
track parameters.
In fact, the 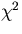 for the track fitting can be written
in the form:
for the track fitting can be written
in the form:
| 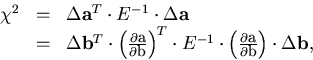 |
(107) |
where in the second line we have diagonalized the error matrix:
| 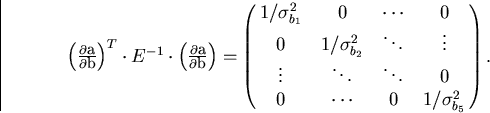 |
(108) |
Since there is now no correlation among bi's, we can
Gaussian-smear them independently:
| 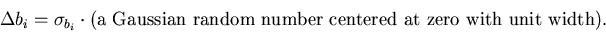 |
(109) |
Then the fluctuation of 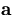 is given by
is given by
| 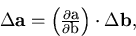 |
(110) |
where the correlations among the parameters are implemented
properly.
Keisuke Fujii
12/4/1998
![]() for the track fitting can be written
in the form:
for the track fitting can be written
in the form: