Change of Pivot

As it will become clear, it is very useful to establish procedure to change pivot positions, since an appropriately chosen pivotal points simplifies calculations necessary, for instance, in energy loss or multiple scattering corrections significantly.

The pivot change

$$\begin{array} {lll} \nonumber {\bf x}_0 = (x_0,y_0,z_0)^T \rightarrow {\bf x}'_0 = (x'_0,y'_0,z'_0)^T\end{array}$$

induces the following change in the helix parameter vector:

$$\begin{array} {lll} \nonumber {\bf a} = (d_\rho,\phi_0,\kap... ...'} = (d'_\rho,\phi'_0,\kappa',d'_z,\tan\lambda')^T ,\end{array}$$

where the new parameters are given in terms of the old ones as follows:  

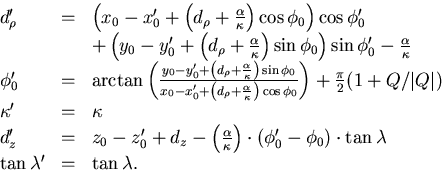$$\begin{array} {lll} d'_\rho & = & \left( x_0 - x'_0 + \le... ... \tan\lambda \cr \tan\lambda' & = & \tan\lambda . \end{array}$$ (9)

The above relations can be readily obtained by requiring the primed parameter vector represents the same helix as the unprimed one. The error matrix should also be transformed accordingly:  

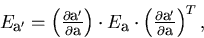$$\begin{array} {lll} E_{\bf a'} = \left(\frac{\partial {\bf ... ...frac{\partial {\bf a'}}{\partial {\bf a}} \right)^T,\end{array}$$ (10)

where the calculation of the transformation (Jacobian) matrix is straightforward from Eq.2.3.14 but it is rather tedious and therefore not shown here.