Unless we have an extra-tracking device in the new region, we do not know the scattering angle in the material. The best we can do is, therefore, to take into account the effect of the multiple scattering on the error matrix.
It can be shown (see Appendix A) that the error matrix for the track extended through the scatterer becomes
| (13) |
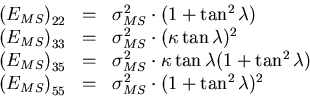 |
(14) |
| |
(15) |
In summary, we can extrapolate a helical track through a material by first moving the pivot to the intersection of the track and the material and then making the aformentioned modifications to the track parameters and error matrix. If there are two or more scatterers, all we have to do is just repeat this process.
Once the error matrix for the extrapolated track is calculated, it is
easy, for instance, to estimate the position error
at a deflection angle ![]() from the error
matrix given by
from the error
matrix given by
| (16) |