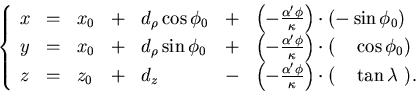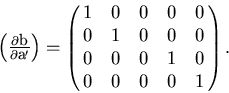Next: Track Linking
Up: Track Extrapolation
Previous: Multiple Scattering Correction
Let us first consider the extrapolation of a track in a
uniform magnetic field  to an adjacent region of a
different magnetic field
to an adjacent region of a
different magnetic field  :
If the pivot is taken at the intersection of the track with the
boundary of the two regions, the helix parameter vector is
left unchanged so is the error matrix, except for the
energy loss and multiple scattering correctoins at the boundary.
:
If the pivot is taken at the intersection of the track with the
boundary of the two regions, the helix parameter vector is
left unchanged so is the error matrix, except for the
energy loss and multiple scattering correctoins at the boundary.
The zero field case corresponds to the infinite 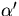 limit,
which implies that
limit,
which implies that 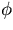 goes to zero while
goes to zero while 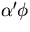 is
kept finite.
Our helix parametrization allows us to take this limit easily.
We expand the helix equations (Eq.2.1.1) in terms of the
deflection angle
is
kept finite.
Our helix parametrization allows us to take this limit easily.
We expand the helix equations (Eq.2.1.1) in terms of the
deflection angle 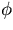 to the first order:
to the first order:
| 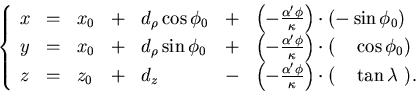 |
(17) |
These become our straight line parametrization,
when we make the replacement:
| 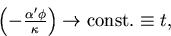 |
(18) |
where the straight line parameter vector is given by
| 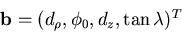 |
(19) |
and their error matrix is obtained by deleting the third row and the
third column of the error matrix for the helix:
| 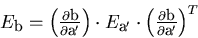 |
(20) |
with
| 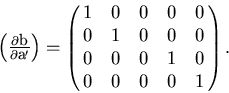 |
(21) |



Next: Track Linking
Up: Track Extrapolation
Previous: Multiple Scattering Correction
Keisuke Fujii
12/4/1998
![]() limit,
which implies that
limit,
which implies that ![]() goes to zero while
goes to zero while ![]() is
kept finite.
Our helix parametrization allows us to take this limit easily.
We expand the helix equations (Eq.2.1.1) in terms of the
deflection angle
is
kept finite.
Our helix parametrization allows us to take this limit easily.
We expand the helix equations (Eq.2.1.1) in terms of the
deflection angle ![]() to the first order:
to the first order: