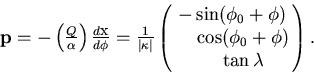Next: Generalities of Track Fitting
Up: General Discussions without Momentum
Previous: General Discussions without Momentum
A charged particle in a uniform magnetic field follows a helical
trajectory.
In what follows we set our reference frame so that it has its
z axis in the direction of the magnetic field.
There are many ways to parametrize this helix.
The following choice, however, greatly facilitates
various operations we are going to make on tracks,
such as track extrapolation and linking:
| 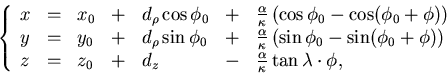 |
(1) |
where
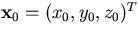 specifies an arbitrarily chosen
pivotal point or simply pivot: we usually take as a pivot
a hit or wire position of the tracking device or a position of
track linking.
Once the pivotal point is fixed, the helix is determined by a
5-component parameter vector
specifies an arbitrarily chosen
pivotal point or simply pivot: we usually take as a pivot
a hit or wire position of the tracking device or a position of
track linking.
Once the pivotal point is fixed, the helix is determined by a
5-component parameter vector
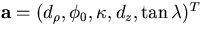 , where
, where
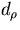 is the distance of the helix from the pivotal point
in the xy plane,
is the distance of the helix from the pivotal point
in the xy plane, 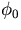 is the azimuthal angle to specifies the
pivotal point with respect to the helix center,
is the azimuthal angle to specifies the
pivotal point with respect to the helix center, 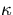 is the
signed reciprocal transverse momentum so that
with Q being the charge,
is the
signed reciprocal transverse momentum so that
with Q being the charge, 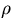 being the signed radius of the
helix, and
being the signed radius of the
helix, and 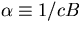 being a
magnetic-field-dependent constant,
dz is the distrance of the helix from the pivotal point in
the z direction, and
being a
magnetic-field-dependent constant,
dz is the distrance of the helix from the pivotal point in
the z direction, and 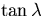 is the dip angle.
The deflection angle
is the dip angle.
The deflection angle 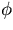 is measured from the pivotal point and
specifies the position of the charged particle on the helical track.
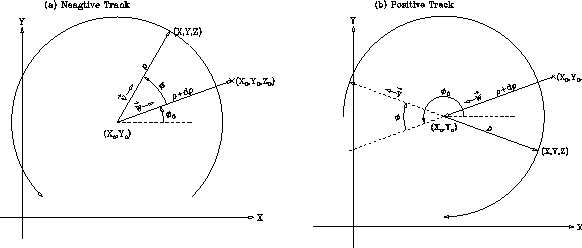
The meanings of these parameters are depicted in Figs.2.1-a)
for negatively charged and -b)
for positively charged particles.
is measured from the pivotal point and
specifies the position of the charged particle on the helical track.
The meanings of these parameters are depicted in Figs.2.1-a)
for negatively charged and -b)
for positively charged particles.![[*]](foot_motif.gif)
Notice that a negatively charged particle travels in the increasing
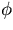 direction, while a positively charged particle travels in
the decreasing
direction, while a positively charged particle travels in
the decreasing 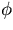 direction.
direction.
Figure 2.1:
A graphical explanation of helix parameters for (a) negatively charged and
(b) positively charged tracks.
Notice that the meaning of
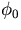 changes discretely by
changes discretely by 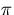 , depending on the charge.
, depending on the charge.
 |
Taking this into account it is easy to get the following formula
which relates the momentum of a charged particle to its helix parameters:
| 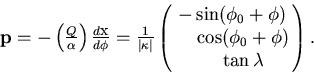 |
(2) |



Next: Generalities of Track Fitting
Up: General Discussions without Momentum
Previous: General Discussions without Momentum
Keisuke Fujii
12/4/1998
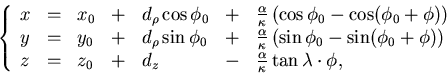
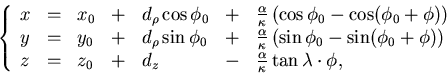
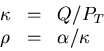
![[*]](foot_motif.gif)
![]() direction, while a positively charged particle travels in
the decreasing
direction, while a positively charged particle travels in
the decreasing ![]() direction.
direction.