W と Z の発見は4点相互作用の理論におけるユニタリティーの問題を解決したが、
標準理論で最も本質的な役割を果たすヒッグスはいまだ発見されておらず、
第2のユニタリィーの破れの問題は未解決である。
LEP 以後ワインバーグ角の精度が著しく向上し、
再び次の実験計画に関する重要なヒントを与えている。
標準理論が予言するのは、色々な実験で決めたワインバーグ角 ![]() が、
0から1までの何処かの値に一致することのみである。
従って、このワインバーグ角の値を正しく予言する理論は、
標準理論を越える理論として極めて有力であるといえる。
が、
0から1までの何処かの値に一致することのみである。
従って、このワインバーグ角の値を正しく予言する理論は、
標準理論を越える理論として極めて有力であるといえる。
標準理論を越える理論として大統一理論(GUT)がある。
前節でふれたように、単一のゲージ群から導かれるゲージ力は
単一の結合定数を持つ。
そこで、もし標準理論のゲージ対称性(41)を
単一のより大きなゲージ群に埋め込むことが出来れば、
強い力、電磁気力、弱い力を統一できる。
もちろん、我々が現在加速器で実験できるようなエネルギーでは
これらの力は異なった大きさを持っているので、
この大きなゲージ群の対称性は、超高エネルギーで自発的に
破れたと考えなくてはならない。
結合定数は、破れずに残った対称性に従い異なった仕方で
エネルギーに依存するので、大統一のエネルギースケール
(![]() )で一致していた結合定数が、
我々が現在実験しているようなエネルギーまで降りてくると、
異なった値を取るようになると考えるのである。
)で一致していた結合定数が、
我々が現在実験しているようなエネルギーまで降りてくると、
異なった値を取るようになると考えるのである。
ここで、何故エネルギーによって力の強さ(結合定数)が変わるのか 直観的に説明しておこう。 不確定性原理によれば、非常に短い時間であれば、エネルギーの不定性は いくらでも大きくなりうる。
| |
(42) |
| (43) |
そのため、たとえば電磁気力の場合は、電子から投げ出された
力の粒子である光子は、瞬間的に電子・陽電子対に化ける。
化ける確率は光子が飛ぶ距離が長いほど高いので、
力の粒子の総数は電子を見る距離が長いほど、
つまり、エネルギーが低いほど、目減りしてしまう(図-6)。
強い相互作用の場合も真空偏極のクォーク・反クォーク対は
遠距離で力の粒子(グルーオン)を減らし、結合定数を
小さくする。
しかし、グルーオンには自己相互作用があり、
グルーオン自体が力の粒子を放出することで、
遠距離ほど力の粒子を増やす。
この効果が打ち勝って、実際には、遠距離ほど
(つまり低エネルギーほど)結合定数が大きくなる(図-7)。
さて、GUT は、ゲージ力の統一を可能にするだけでなく、
電荷の量子化やアノーマリーの相殺等、
標準理論では説明できないことに合理的な説明を与える。
しかし、標準理論を含む最小の GUT である SU(5) 理論は、
良く知られた自然さの問題を抱えている。
これは、ヒッグス粒子の質量に対する量子補正が理論の
自然なスケール(![]() )
程度の大きさを持つため、ラグランジアンに入れておく
裸のヒッグス粒子の質量パラメータを
二十数桁にわたって微調整しておかなければ、
GUT スケールから我々のエネルギーに降りてきたときに、
現実世界が再現できないという問題である。
このような微調整は非常に不自然である(我々の世界は
ものすごい偶然の結果生じたことになる)。
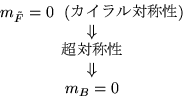
これは、スピン 1/2 の物質粒子にはカイラル対称性、ゲージ粒子には
ゲージ対称性があり、エネルギーが高くなって対称性が回復すると
質量に対する量子補正が大きくなれないのに対し(40)、
ヒッグス粒子のようなスピン 0 のスカラー粒子には、
質量をゼロにするような対称性がないためである。
)
程度の大きさを持つため、ラグランジアンに入れておく
裸のヒッグス粒子の質量パラメータを
二十数桁にわたって微調整しておかなければ、
GUT スケールから我々のエネルギーに降りてきたときに、
現実世界が再現できないという問題である。
このような微調整は非常に不自然である(我々の世界は
ものすごい偶然の結果生じたことになる)。
これは、スピン 1/2 の物質粒子にはカイラル対称性、ゲージ粒子には
ゲージ対称性があり、エネルギーが高くなって対称性が回復すると
質量に対する量子補正が大きくなれないのに対し(40)、
ヒッグス粒子のようなスピン 0 のスカラー粒子には、
質量をゼロにするような対称性がないためである。
この問題は、さらに新しい対称性(超対称性)を加えることで解決される。
超対称性はフェルミオン(半整数スピン粒子)とボソン(整数スピン粒子)
を同一粒子の異なる状態と見なすような対称性である(図-8)。
理論が超対称性を持てば、もちろん対応するフェルミオンとボソンの 質量は等しい。 そこで、スカラーボソンであるヒッグス粒子の相棒のスピン 1/2 の 超粒子の質量がカイラル対称性で守られているために、 ヒッグス粒子の質量補正も発散しなくなるのである。
 |
(44) |
驚くべきことは、自然さの問題を解決するために導入された超対称性が、 同時に力の統一の成立に決定的な役割を果たすことである。
図-9a は標準理論のゲージ対称性(41)に対応する
3つの結合定数 ![]() 、
、![]() 、
、![]() の測定値から、
それらの高エネルギーでの値を予測したものである。
の測定値から、
それらの高エネルギーでの値を予測したものである。