

Next: �桹��õ�᤹�٤������о����ϲ��ʤΤ���
Up: �����������Ȥϡ�
Previous: �ɽꥲ�����о�������
����23�ˤ�
�⤦������ܤ��٤��ʤΤϡ�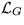 ��������γ�Ҥμ��̹��
�ޤޤʤ����Ǥ��롣
�ºݡ����̹�
��������γ�Ҥμ��̹��
�ޤޤʤ����Ǥ��롣
�ºݡ����̹�
| 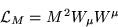 |
(26) |
�ϡ�������γ�Ҥ��Ф��륲�����Ѵ���16�ˤ��Ф������餫��
���ѤǤʤ���
�Ĥޤꡢ�������о����ϡ�������γ�Ҥ����̤���Ĥ��Ȥ�
�ػߤ��Ƥ���ΤǤ��롣
�桹���ΤäƤ�����̤�����ʤ��٥��ȥ�γ�Ҥϸ��Ҥ����ʤΤǡ�
���ΤޤޤǤϡ��������������ŵ��ϳؤˤ���Ŭ�ѤǤ��ʤ���
��������顢��������̿Ū�ʷ�٤��Ȼפ��Ƥ�����
�饰�����Υ������о������ݤ��Ĥġ�������γ�Ҥ˼��̤�Ϳ���뤳�Ȥ�
��ǽ�Ȥ����Τ��ּ�ȯŪ�о������ˤ�פιͤ����Ǥ��롣
����Ū�ʥ����ǥ��ϡ��־��������̵�¼�ͳ�٤Ǥ��뤿��ˡ�
�饰�������о�����ɬ�����⸽�ݤ��о������̣���ʤ��פ��Ȥ�
���ܤ��뤳�ȤǤ��롣
�ޤ���������γ�Ҥȥ�������ߺ��Ѥ��륹���顼��
��ʣ�ǣ������Υҥå�����: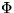 �ˤ�
Ƴ�����롣
�ҥå�����Υݥƥ��
�ˤ�
Ƴ�����롣
�ҥå�����Υݥƥ�� 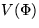 ����
��-2 �Τ褦�ʷ��Ƥ����硢
����
��-2 �Τ褦�ʷ��Ƥ����硢
| 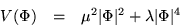 |
(27) |
�ʤ�������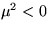 ��
��ͤ��롣
��
��ͤ��롣
Figure 2:
�ҥå����ݥƥ��
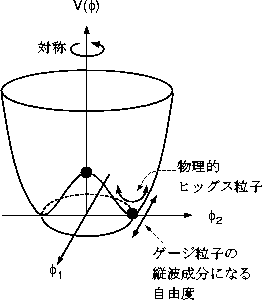 |
�饰�������о����ϡ����Υҥå�����Υݥƥ�뤬
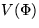 ���β����оΤǤ��뤳�Ȥ��̣���Ƥ��롣
���ξ��Ϥ�������
����(���ͥ륮������ξ��֡ˤ�����˽��ष�Ƥ��롣
���β����оΤǤ��뤳�Ȥ��̣���Ƥ��롣
���ξ��Ϥ�������
����(���ͥ륮������ξ��֡ˤ�����˽��ष�Ƥ��롣
�ºݤ˼¸����Ƥ��뿿���Ϥ����Σ��ĤǤ��뤿�ᡢ
�����������ִ֤��о������ˤ��
�ʤ��ο����ϡ�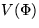 ���β��β�ž�ǥ����̤����ذܤ����ѤǤʤ��ˡ�
���פʤΤϡ����ξ��ο�����ͭ�¤Υҥå�����
(
���β��β�ž�ǥ����̤����ذܤ����ѤǤʤ��ˡ�
���פʤΤϡ����ξ��ο�����ͭ�¤Υҥå�����
(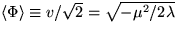 )����������Ƥ��뤳�ȤǤ���
�ʥ����顼���Ȥä��Τϡ�������Ʊ���̻ҿ�����äƤ��ʤ��ȡ�
������˶Ž̤Ǥ��ʤ�����Ǥ���ˡ�
)����������Ƥ��뤳�ȤǤ���
�ʥ����顼���Ȥä��Τϡ�������Ʊ���̻ҿ�����äƤ��ʤ��ȡ�
������˶Ž̤Ǥ��ʤ�����Ǥ���ˡ�
�������ҥå���γ�Ҥȥ�����γ�Ҥ���ߺ��Ѥϡ������������Ƿ��ꤵ�졢
�����顼γ�ҤΥ饰�����ǡ�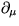 ��
�� 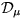 ���֤����������
���֤����������
| 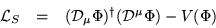 |
(28) |
����Ƴ����롣
���פʤΤϡ���-3 �˼�������ߺ��ѤǤ��롣
Figure 3:
�ҥå�����ȥ��������W�ˤΣ�����������ߺ���
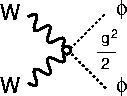 |
���οޤǥҥå��������ʬ��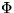 �ˤο���������
��
�ˤο���������
��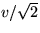 �ˤ��֤�������ȡ�
�ˤ��֤�������ȡ�
| 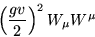 |
(29) |
���μ��̹ब����롣
�Ĥޤꡢ������γ�� 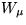 ����
����
| 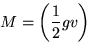 |
(30) |
�ʤ���̤�����������Ȥˤʤ롣
���̤Τʤ��٥��ȥ�γ�ҤˤϽ�����ʬ��̵����ͳ�٤ϣ��Ǥ��뤬��
���̤��������Ƚ�����ʬ��������ͳ�٤����ˤʤ롣
����;ʬ�μ�ͳ�٤ϡ��ҥå����ݥƥ���
ʿ��������Ρʽ��äƼ��̤�����ʤ��˥ҥå������
��ͳ�١ʿ�-2�ˤˤ�äƶ��뤵��롣
ʿ��������μ�ͳ�٤��ˤ줿�о����ο��ʤ��������ؤ��Ѵ���
�����Ҥο��ˤ������롣
���Τʤ餽�������ؤ��Ѵ��ǿ��������ѤǤʤ�����Ǥ��롣
���μ�ͳ�٤��̾若����ɥ��ȡ���⡼�ɤȸƤ֡�
ʿ��Ǥʤ������μ�ͳ�٤ϼ��̤���ä�ʪ��Ū
�ҥå���γ�ҤȤʤ롣
���Υҥå���γ�Ҥμ��̤ϡ��ݥƥ��ζ�Ψ�Ƿ�ޤꡢ
| 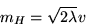 |
(31) |
��Ϳ�����롣
�ʾ�μ������������ϡ�ľ��Ū�ˤϼ��Τ褦�˲��Ǥ��롣
���̤Ȥϡ���®����ˤ�����ɽ���̤Ǥ��롣
�����˶Ž̤����ҥå�����γ�����ǡ�������γ�Ҥ��®���褦�Ȥ����
�ҥå�����ˤ֤Ĥ��ä�������롣
�����ϥ������줬���ĤΥҥå����Ⱦ��ͤ������٤�ɽ��
������(g)�ȡ�������Υҥå�����̩��(v)�����㤹��Ϥ��Ǥ��롣
���äơ�
| 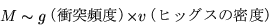 |
(32) |
�Ȥʤ�ʿ�-4�ˡ�
Figure 4:
�ҥå��������ˤ���������
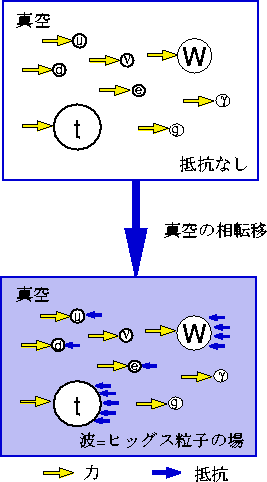 |
���Τ褦�ʼ�������������֥ҥå��������פȸƤ֡�
������γ�Ҥμ��̤����Ǥʤ�ʪ��γ�Ҥμ��̤⡢�ҥå����������������
����Τ�ɸ�������ιͤ����Ǥ��롣
�¤ϡ�ɸ�������ξ�硢ʪ��γ�Ҥ�饰�������ʳ��Ǥϼ��̤�
���Ƥʤ���
�饰������24�ˤǡ����̹�
| 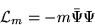 |
(33) |
�������줿�Τϡ�������γ�Ҿ��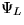 �ˤȱ�����γ�Ҿ��
�ˤȱ�����γ�Ҿ��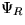 �ˤ���
Ʊ���������о�������ĤȰŤ˲��ꤷ�Ƥ�������Ǥ��롣
��������
�ˤ���
Ʊ���������о�������ĤȰŤ˲��ꤷ�Ƥ�������Ǥ��롣
��������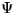 ��
��
| 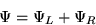 |
(34) |
��Ϳ����졢
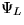 ��
�� 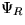 �ϡ�
�ϡ�
| 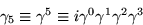 |
(35) |
�Ȥ��ơ�
| 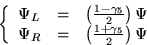 |
(36) |
���������롣
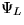 ��
�� 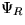 ���Ѥ���ȡ�����33�ˤϡ�
���Ѥ���ȡ�����33�ˤϡ�
| 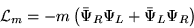 |
(37) |
�Ȥʤ롣
�����ǡ�
| 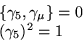 |
(38) |
��Ȥä���
����37�ˤϡ����̹ब������γ�Ҿ����γ�Ҿ�ء�������γ�Ҿ��
������γ�Ҿ�ؤȡ�ž�����뤳�Ȥ��̣���Ƥ��롣
����ϡ�ľ��Ū�ˤϼ��Τ褦�������Ǥ��롣
���̤�����ʤ�γ�ҤϾ�˸�®�DZ�ư���롣
��®�DZ�ư����γ�Ҥ��ɤ��ۤ����ȤϽ���ʤ���
���������̤���ä�γ�Ҥ��ɤ��ۤ��롣
�ɤ��ۤ��Ƥ��餽��γ�Ҥ�ȡ�
��ư��������ž����Τǡʥ��ԥ�θ����Ϥ��Τޤޡˡ�
�������Ⱥ��������������롣
�ɤ��ۤ��ʤ���Ф��ΤޤޤǤ��롣
���ơ����̹ब�������Ⱥ�������ž������Τ��Ф���
�饰������24�ˤ�ʪ��γ�Ҿ��ޤ�¾����ʬ
| 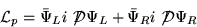 |
(39) |
�ϱ������Ⱥ���������碌�뤳�ȤϤʤ���
�����ǡ����̹ब̵����С�
�������Ⱥ��������Ф��ơ��̡��ΰ����Ѵ���ܤ��Ƥ⡢
�饰���������ѤȤʤ�ʥ�������о����ˡ�
�Ĥޤꡢ������γ�Ҿ�Ⱥ�����γ�Ҿ�Ȥϡ��̤�γ�Ҥȸ��ʤ������äơ��̤�
�о�������������롣
�դˡ��������Ⱥ����������̡����о�������Ĥ���ˤϡ�
�饰��������ʪ��γ�Ҥμ��̹�϶ػߤ���롣
ɸ�������ϡ��ޤ��ˤ��Τ褦�������Ǥ��äơ�
����12�ˤ˼��������Ź��°����Τϡ�
������γ�ҡ�ź���� L�ˤΤߤǡ��б����뱦����γ�Ҥϣ��Ź�
��°���Ƥ��롣
���¤�ʪ��γ�Ҥϼ��̤���äƤ���Τǡ��饰�����Υ������о�����
�ݤä��ޤ�ʪ��γ�Ҥμ��̤�Ƴ������ˤϡ��ҥå���������ɬ�פȤʤ�ΤǤ��롣
���פʤΤϡ�������γ�Ҥμ��������ϥҥå���γ�Ҥȥ�����γ�Ҥδ֤�
����Ū�ʥ�������ߺ��Ѥˤ���ΤǤ���Τ��Ф���
ʪ��γ�Ҥμ��������ˤϡ��ҥå���γ�ҤȤδ֤�������ߺ��ѤȸƤФ��
��������ߺ��Ѥ�Ƴ�����ʤ���Фʤ�ʤ����Ǥ��롣
����������ߺ��Ѥϡ�ʪ��γ�Ҥμ��������亮����������������
��������ߺ��ѤΤ褦��ɬ����������ʤ��Τǡ�¬�ꤵ�줿
ʪ��γ�Ҥΰۤʤ���̤亮��Ѥ��б�����γ�Ҥο��䡢����Ѥο�����
�ۤʤä����������ꤷ�ʤ��ƤϤʤ�ʤ���
�ޤȤ���
|  |
(40) |
�Ȥʤ롣


Next: �桹��õ�᤹�٤������о����ϲ��ʤΤ���
Up: �����������Ȥϡ�
Previous: �ɽꥲ�����о�������
Keisuke Fujii
5/2/2000
![]() ��������γ�Ҥμ��̹��
�ޤޤʤ����Ǥ��롣
�ºݡ����̹�
��������γ�Ҥμ��̹��
�ޤޤʤ����Ǥ��롣
�ºݡ����̹�
![]() �ˤ�
Ƴ�����롣
�ҥå�����Υݥƥ��
�ˤ�
Ƴ�����롣
�ҥå�����Υݥƥ�� ![]() ����
��-2 �Τ褦�ʷ��Ƥ����硢
����
��-2 �Τ褦�ʷ��Ƥ����硢
![]() ���β��β�ž�ǥ����̤����ذܤ����ѤǤʤ��ˡ�
���פʤΤϡ����ξ��ο�����ͭ�¤Υҥå�����
(
���β��β�ž�ǥ����̤����ذܤ����ѤǤʤ��ˡ�
���פʤΤϡ����ξ��ο�����ͭ�¤Υҥå�����
(![]() )����������Ƥ��뤳�ȤǤ���
�ʥ����顼���Ȥä��Τϡ�������Ʊ���̻ҿ�����äƤ��ʤ��ȡ�
������˶Ž̤Ǥ��ʤ�����Ǥ���ˡ�
)����������Ƥ��뤳�ȤǤ���
�ʥ����顼���Ȥä��Τϡ�������Ʊ���̻ҿ�����äƤ��ʤ��ȡ�
������˶Ž̤Ǥ��ʤ�����Ǥ���ˡ�
![]() ��
�� ![]() ���֤����������
���֤����������
