

Next: 自発的対称性の破れ
Up: ゲージ原理とは?
Previous: 対称性と粒子の統一
粒子の統一を考慮して、複数個の量子場を混ぜ合わせるような
一般的な位相変換(ゲージ変換と呼ぶ)に対し、
その混ぜ合わせ方を時空の各点で勝手に変えてもラグランジアンが不変になる
べしと言う要請に立ち戻ろう。
自由場のラグランジアン(4)は、既に指摘したとおりこの要請を
満たさない(記法の簡便化のため、これ以後、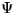 は複数個の量子場を
まとめて表したものとする)。
は複数個の量子場を
まとめて表したものとする)。
その理由は、式(9)のように、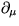 と
と
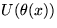 が交換しないことであった。
ようするに、
が交換しないことであった。
ようするに、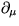 の代わりに
の代わりに
| 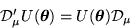 |
(13) |
となるような共変微分 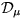 を見つければよい。
そこで、g をある1つの定数として
を見つければよい。
そこで、g をある1つの定数として
| 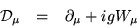 |
(14) |
と置いてみる。
ここで、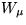 はローレンツの足を持った(ゲージ場と呼ばれる)
ベクトル場で、
はローレンツの足を持った(ゲージ場と呼ばれる)
ベクトル場で、
| 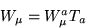 |
(15) |
のように、変換群(ゲージ群)の生成子(Ta; a=1,...,n)で展開され、
従って生成子の数だけ独立な成分を持っている。
さて、
| 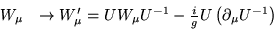 |
(16) |
であれば、式(13)を満足することは容易に分かる。
つまり、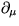 を
を 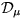 で置き換えた新しいラグランジアン
で置き換えた新しいラグランジアン
| 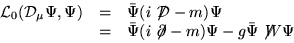 |
(17) |
は、一般化された局所位相変換に対して不変となる。
注目すべきなのは、右辺の最後の項である。
この項は、新しく導入したゲージ場(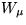 )と、物質場 (
)と、物質場 (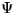 )との
相互作用を表している。
定数(g)は結合定数と呼ばれ、ゲージ場と物質場の間の
相互作用の大きさを決める。
ゲージ群が電気力学の U(1) 場合には、結合定数は電子の電荷
の絶対値となり、ゲージ場は、光子の場に対応する。
)との
相互作用を表している。
定数(g)は結合定数と呼ばれ、ゲージ場と物質場の間の
相互作用の大きさを決める。
ゲージ群が電気力学の U(1) 場合には、結合定数は電子の電荷
の絶対値となり、ゲージ場は、光子の場に対応する。
つまり、局所的な一般位相変換 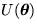 の
もとでのラグランジアンの不変性は、ゲージ場の存在論理を与えるのみならず、
ゲージ場と物質粒子の間の相互作用を決定してしまうのである。
物質粒子同士の相互作用(力)はこのゲージ場に対応するゲージ粒子を
交換することによって生じる。
つまり、対称性と力の間には本質的な関係があることになる。
強調すべき事は、結合定数(g)は、ゲージ群1つにつき1つ
である点である。
これは、ゲージ群の1つの多重項に属する物質粒子間の相互作用が
同じ強さを持った単一の力であることを意味する。
この力の普遍性は、ゲージ相互作用の著しい特徴である。
これはまた、力の統一に関する重要なヒントを含んでいる。
力がゲージ粒子の交換であれば、異なった力の粒子を
1つのゲージ群のゲージ場の異なった成分だと見なせれば、
力が統一されるからである。
この問題については、また後で議論しよう。
の
もとでのラグランジアンの不変性は、ゲージ場の存在論理を与えるのみならず、
ゲージ場と物質粒子の間の相互作用を決定してしまうのである。
物質粒子同士の相互作用(力)はこのゲージ場に対応するゲージ粒子を
交換することによって生じる。
つまり、対称性と力の間には本質的な関係があることになる。
強調すべき事は、結合定数(g)は、ゲージ群1つにつき1つ
である点である。
これは、ゲージ群の1つの多重項に属する物質粒子間の相互作用が
同じ強さを持った単一の力であることを意味する。
この力の普遍性は、ゲージ相互作用の著しい特徴である。
これはまた、力の統一に関する重要なヒントを含んでいる。
力がゲージ粒子の交換であれば、異なった力の粒子を
1つのゲージ群のゲージ場の異なった成分だと見なせれば、
力が統一されるからである。
この問題については、また後で議論しよう。
ここでは、これまでの議論の直観的な解釈を試みてみよう。
量子力学によれば、粒子は波動性を持つ。
運動量の固有状態にある自由粒子なら、平面波で表される。
| 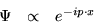 |
(18) |
ただし、指数部は
| 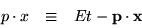 |
(19) |
であり、運動量と波長の間にはドブローイの関係
| 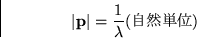 |
(20) |
が成り立っている。
そこで、時空の各点での勝手な位相変換は粒子の波長に変調をかけ、
従ってそのままでは運動量が保存しなくなってしまう。
ある点での波長は、同時刻でのその点から無限小だけ
離れた点との位相差で決まるので、運動量を保存させるには、
位相の原点をゲージ変換に合わせて各点毎に独立に決めてやれば良い。
共変微分の形が示すとおり、
この位相の基準となるのがまさにゲージ場なのである。
さて、式(17)で与えられるラグランジアンには、
自由ゲージ場のラグランジアン(ゲージ場の運動項)が含まれていない。
ところが、このゲージ場の運動項も、やはり、
局所ゲージ変換に対する不変性の要請から決まってしまう。
容易に分かるように、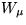 から作られるテンソル場
から作られるテンソル場
| ![\begin{displaymath}
\begin{array}
{lll}
W_{\mu\nu} & = & - \frac{i}{g} \left[ {...
...\partial_\nu W_\nu
+ ig \left[ W_\mu, W_\nu \right]\end{array}\end{displaymath}](img39.gif) |
(21) |
は、
| 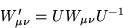 |
(22) |
のように共変的に変換するので、
| 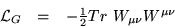 |
(23) |
は、局所ゲージ不変である。
ここで注目すべきは、式(21)の第3項のために、上の
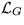 は、ゲージ群が非可換の場合、
は、ゲージ群が非可換の場合、
 に関する3次と4次の項、すなわち、
ゲージ粒子同士の自己相互作用を含む点である。
この相互作用の形も強さ(結合定数)も
ゲージ対称性により決まってしまう。
結局、物質粒子の部分(17)とゲージ粒子の部分(23)を
合わせて、
に関する3次と4次の項、すなわち、
ゲージ粒子同士の自己相互作用を含む点である。
この相互作用の形も強さ(結合定数)も
ゲージ対称性により決まってしまう。
結局、物質粒子の部分(17)とゲージ粒子の部分(23)を
合わせて、
| 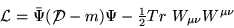 |
(24) |
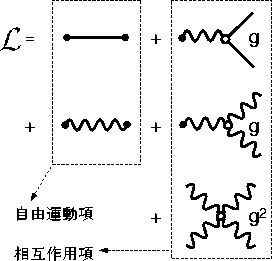
となる(図-1)は、このラグランジアンを図示したものである)。
Figure 1:
ゲージ理論のラグランジアン
 |
このゲージ対称性がラグランジアンを決定すると言う考え方
(対称性と力の本質的関係)をゲージ原理と呼ぶ。
|  |
(25) |


Next: 自発的対称性の破れ
Up: ゲージ原理とは?
Previous: 対称性と粒子の統一
Keisuke Fujii
5/2/2000
![]() は複数個の量子場を
まとめて表したものとする)。
は複数個の量子場を
まとめて表したものとする)。
![]() と
と
![]() が交換しないことであった。
ようするに、
が交換しないことであった。
ようするに、![]() の代わりに
の代わりに
![]() の
もとでのラグランジアンの不変性は、ゲージ場の存在論理を与えるのみならず、
ゲージ場と物質粒子の間の相互作用を決定してしまうのである。
物質粒子同士の相互作用(力)はこのゲージ場に対応するゲージ粒子を
交換することによって生じる。
つまり、対称性と力の間には本質的な関係があることになる。
強調すべき事は、結合定数(g)は、ゲージ群1つにつき1つ
である点である。
これは、ゲージ群の1つの多重項に属する物質粒子間の相互作用が
同じ強さを持った単一の力であることを意味する。
この力の普遍性は、ゲージ相互作用の著しい特徴である。
これはまた、力の統一に関する重要なヒントを含んでいる。
力がゲージ粒子の交換であれば、異なった力の粒子を
1つのゲージ群のゲージ場の異なった成分だと見なせれば、
力が統一されるからである。
この問題については、また後で議論しよう。
の
もとでのラグランジアンの不変性は、ゲージ場の存在論理を与えるのみならず、
ゲージ場と物質粒子の間の相互作用を決定してしまうのである。
物質粒子同士の相互作用(力)はこのゲージ場に対応するゲージ粒子を
交換することによって生じる。
つまり、対称性と力の間には本質的な関係があることになる。
強調すべき事は、結合定数(g)は、ゲージ群1つにつき1つ
である点である。
これは、ゲージ群の1つの多重項に属する物質粒子間の相互作用が
同じ強さを持った単一の力であることを意味する。
この力の普遍性は、ゲージ相互作用の著しい特徴である。
これはまた、力の統一に関する重要なヒントを含んでいる。
力がゲージ粒子の交換であれば、異なった力の粒子を
1つのゲージ群のゲージ場の異なった成分だと見なせれば、
力が統一されるからである。
この問題については、また後で議論しよう。