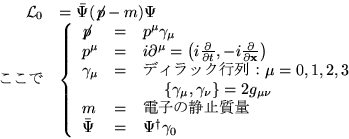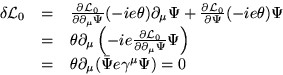

Next: 対称性と粒子の統一
Up: ゲージ原理とは?
Previous: ゲージ原理とは?
現在、素粒子の世界を記述するのに用いられている基本的な言葉は、場の量子論である。
これは、言わば自然の語る言葉の文法であって、問題とする客体に固有な性質は全て
ラグランジアンに含まれている。
つまり
| 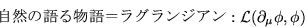 |
(1) |
と言うことになる(ここで、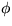 は基本粒子の場をまとめて表したものである)。
実際、
は基本粒子の場をまとめて表したものである)。
実際、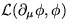 が与えられれば、変分原理から
オイラー・ラグランジュ方程式として場の運動方程式
が与えられれば、変分原理から
オイラー・ラグランジュ方程式として場の運動方程式
| 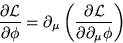 |
(2) |
が得られ問題とする客体の時間発展が(少なくとも原理的には)追えることになる。
そこで我々が知りたいのは、この自然の物語のテーマが何かである。
ネーターの定理として有名なラグランジアンの対称性と保存則の関係は、
「自然の語る物語の中心テーマが対称性なのではないか?」と思わせる最初の
深遠な結果である(例えば、エネルギー・運動量保存則や角運動量保存則が、
時空の対称性の帰結である事は良く知られている)。
ラグランジアンの対称性(すなわち、量子場(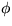 )のある種の変換
に対するラグランジアンの不変性)の要求は、可能な
)のある種の変換
に対するラグランジアンの不変性)の要求は、可能な 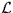 の形を
強く制限する。そこで、「十分多くの対称性を要求すれば、
の形を
強く制限する。そこで、「十分多くの対称性を要求すれば、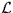 が
一意に決まるのではないか?」と言う予想が成り立つ。
実際、ウイグナーは、時空の対称性(並進群
が
一意に決まるのではないか?」と言う予想が成り立つ。
実際、ウイグナーは、時空の対称性(並進群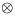 ローレンツ群=ポアンカレ群)
が、可能な自由粒子場のラグランジアンの形を完全に規定してしまうことを示した。
ローレンツ群=ポアンカレ群)
が、可能な自由粒子場のラグランジアンの形を完全に規定してしまうことを示した。
| 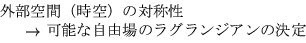 |
(3) |
相互作用まで含めたラグランジアンの決定には、しかし、外部空間の対称性
だけでは不十分で、内部空間の対称性を知る必要がある。
ここで内部空間と呼んだのは、時空の各点での量子場の自由度に対応する
空間のことである。
保存則のあるところに対称性があるのだから、内部空間の対称性を見つけるには、
エネルギー・運動量・角運動量等の外部空間の対称性に起因する保存則以外の
保存則に注目すればよい。
このような保存則として、電荷の保存は良く知られた例である。
実際、自由電子場のラグランジアン
| 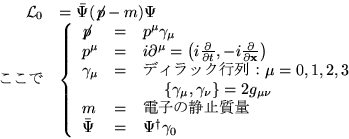 |
(4) |
(これ以降自然単位 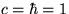 )は、時空中の位置(x)によらない位相変換
)は、時空中の位置(x)によらない位相変換
| 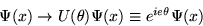 |
(5) |
により、
| 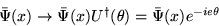 |
(6) |
から、明らかに不変であるが、
これから 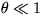 として
次のように電荷の保存則が導かれる。
として
次のように電荷の保存則が導かれる。
| 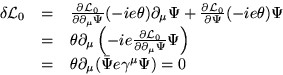 |
(7) |
ただし一行目から二行目で (2)、二行目から
三行目で (4) を用いた。
最後の式のかっこの中が保存される4元電流密度である。
まとめると、
位相の基準点の変更が物理を変えないと言う要求から、ネーターの定理により
電荷の保存則が導かれたことになる。
|  |
(8) |


Next: 対称性と粒子の統一
Up: ゲージ原理とは?
Previous: ゲージ原理とは?
Keisuke Fujii
5/2/2000
![]() )のある種の変換
に対するラグランジアンの不変性)の要求は、可能な
)のある種の変換
に対するラグランジアンの不変性)の要求は、可能な ![]() の形を
強く制限する。そこで、「十分多くの対称性を要求すれば、
の形を
強く制限する。そこで、「十分多くの対称性を要求すれば、![]() が
一意に決まるのではないか?」と言う予想が成り立つ。
実際、ウイグナーは、時空の対称性(並進群
が
一意に決まるのではないか?」と言う予想が成り立つ。
実際、ウイグナーは、時空の対称性(並進群![]() ローレンツ群=ポアンカレ群)
が、可能な自由粒子場のラグランジアンの形を完全に規定してしまうことを示した。
ローレンツ群=ポアンカレ群)
が、可能な自由粒子場のラグランジアンの形を完全に規定してしまうことを示した。