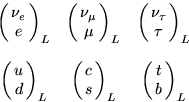

Next: 局所ゲージ対称性と力
Up: ゲージ原理とは?
Previous: 対称性と保存則
位相の基準点の変更が物理を変えないと言うことは、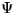 で表される
粒子と
で表される
粒子と 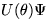 で表される粒子が、物理的に区別できないことを
意味している。
しかし、ここでの位相変換が、時空中の位置(x)によらない大局的な位相変変換
(つまり、宇宙全体で一斉に位相の基準点を同じだけ変えること)である点に
注意する必要がある。
で表される粒子が、物理的に区別できないことを
意味している。
しかし、ここでの位相変換が、時空中の位置(x)によらない大局的な位相変変換
(つまり、宇宙全体で一斉に位相の基準点を同じだけ変えること)である点に
注意する必要がある。
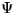 で表される
粒子と
で表される
粒子と 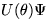 で表される粒子が物理的に区別できないのであれば、
時空の各点で勝手に位相変換しても物理は不変であって欲しい。
ところが、
で表される粒子が物理的に区別できないのであれば、
時空の各点で勝手に位相変換しても物理は不変であって欲しい。
ところが、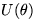 中の
中の 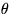 を時空の各点に依存する
を時空の各点に依存する
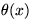 とすると、もはやラグランジアン(4)は不変ではなくなる。
とすると、もはやラグランジアン(4)は不変ではなくなる。
| 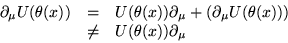 |
(9) |
となるからである。これははなはだ不満足である。
もう一つ注目すべきなのは、変換 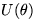 に対するラグランジアンの対称性が
に対するラグランジアンの対称性が
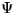 で表される粒子と
で表される粒子と 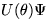 で表される粒子が物理的に
区別できないことを意味しているという点自体である。
これは、今の場合、
で表される粒子が物理的に
区別できないことを意味しているという点自体である。
これは、今の場合、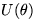 が単なる位相変換
(1次元ユニタリー群:U(1))であったので
トリビアルかも知れないが、粒子の統一に関する重要なヒントを含んでいる。
例えば、2種類の粒子があったとしよう。
これらに対応する量子場を
が単なる位相変換
(1次元ユニタリー群:U(1))であったので
トリビアルかも知れないが、粒子の統一に関する重要なヒントを含んでいる。
例えば、2種類の粒子があったとしよう。
これらに対応する量子場を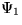 と
と 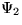 とすれば、
行列式が1であるような2次元ユニタリー行列による
とすれば、
行列式が1であるような2次元ユニタリー行列による 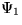 と
と 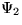 を
混ぜ合わせるような一般化された位相変換(SU(2) 対称性)
を
混ぜ合わせるような一般化された位相変換(SU(2) 対称性)
| 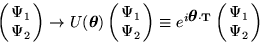 |
(10) |
のもとでのラグランジアンの不変性(SU(2) 対称性)は、
その2種類の粒子が区別できないこと、
すなわち、同じ粒子の異なった状態にすぎないことを意味する。
ただし、
| 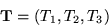 |
(11) |
は、SU(2) 群の生成子である。
例えば標準理論の基本粒子をレプトン、クォーク各々、2重項にまとめて
| 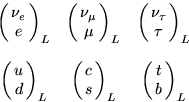 |
(12) |
と書くとき、かっこにまとめられた粒子対が統一されていることを意味している。


Next: 局所ゲージ対称性と力
Up: ゲージ原理とは?
Previous: 対称性と保存則
Keisuke Fujii
5/2/2000
![]() で表される
粒子と
で表される
粒子と ![]() で表される粒子が、物理的に区別できないことを
意味している。
しかし、ここでの位相変換が、時空中の位置(x)によらない大局的な位相変変換
(つまり、宇宙全体で一斉に位相の基準点を同じだけ変えること)である点に
注意する必要がある。
で表される粒子が、物理的に区別できないことを
意味している。
しかし、ここでの位相変換が、時空中の位置(x)によらない大局的な位相変変換
(つまり、宇宙全体で一斉に位相の基準点を同じだけ変えること)である点に
注意する必要がある。
![]() で表される
粒子と
で表される
粒子と ![]() で表される粒子が物理的に区別できないのであれば、
時空の各点で勝手に位相変換しても物理は不変であって欲しい。
ところが、
で表される粒子が物理的に区別できないのであれば、
時空の各点で勝手に位相変換しても物理は不変であって欲しい。
ところが、![]() 中の
中の ![]() を時空の各点に依存する
を時空の各点に依存する
![]() とすると、もはやラグランジアン(4)は不変ではなくなる。
とすると、もはやラグランジアン(4)は不変ではなくなる。
![]() に対するラグランジアンの対称性が
に対するラグランジアンの対称性が
![]() で表される粒子と
で表される粒子と ![]() で表される粒子が物理的に
区別できないことを意味しているという点自体である。
これは、今の場合、
で表される粒子が物理的に
区別できないことを意味しているという点自体である。
これは、今の場合、![]() が単なる位相変換
(1次元ユニタリー群:U(1))であったので
トリビアルかも知れないが、粒子の統一に関する重要なヒントを含んでいる。
例えば、2種類の粒子があったとしよう。
これらに対応する量子場を
が単なる位相変換
(1次元ユニタリー群:U(1))であったので
トリビアルかも知れないが、粒子の統一に関する重要なヒントを含んでいる。
例えば、2種類の粒子があったとしよう。
これらに対応する量子場を![]() と
と ![]() とすれば、
行列式が1であるような2次元ユニタリー行列による
とすれば、
行列式が1であるような2次元ユニタリー行列による ![]() と
と ![]() を
混ぜ合わせるような一般化された位相変換(SU(2) 対称性)
を
混ぜ合わせるような一般化された位相変換(SU(2) 対称性)