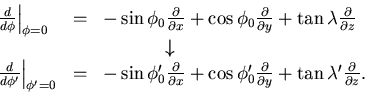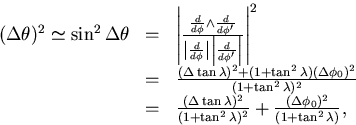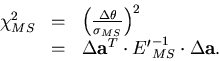Next: Measurement Error Matrix at
Up: No Title
Previous: Summary
Consider a particle passing through a thin layer, whose
track parameter vector changes from  to
to 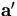 due to multiple scattering there.
We assume here that the track parameter vector of the particle
is measured after the multiple scattering to be
due to multiple scattering there.
We assume here that the track parameter vector of the particle
is measured after the multiple scattering to be 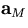 with its error matrix
with its error matrix 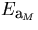
![[*]](foot_motif.gif) .
In the Gaussian approximation valid for small angle multiple scattering,
the probability of getting
.
In the Gaussian approximation valid for small angle multiple scattering,
the probability of getting 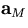 when the true track parameter
vector before the multiple scattering is
when the true track parameter
vector before the multiple scattering is 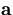 is given by
is given by
| ![\begin{displaymath}
\begin{array}
{lll}
P\left({\bf a}_M;{\bf a}\right)
& = & ...
...left( {\bf a} - {\bf a}'' \right)
\right) \right],\end{array}\end{displaymath}](img252.gif) |
(1) |
where E'MS is the diagonalized error matrix corresponding to
multiple scattering![[*]](foot_motif.gif) N is a normalization factor depending only on
N is a normalization factor depending only on
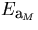 and E'MS, and
with B being a matrix whose only nonzero component is
and E'MS, and
with B being a matrix whose only nonzero component is
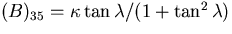 .Making use of the fact that B is nilpotent, i.e.
B2 = 0, we can easily eliminate
.Making use of the fact that B is nilpotent, i.e.
B2 = 0, we can easily eliminate 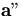 from
the exponent of Eq.A.1:
from
the exponent of Eq.A.1:
| 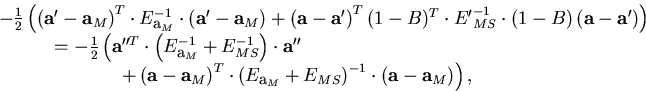 |
(3) |
where we have defined
| 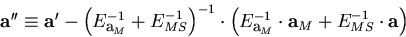 |
(4) |
and
| ![\begin{displaymath}
\begin{array}
{lll}
E_{MS}^{-1} & \equiv & (1-B)^T {E'}_{MS...
...
& = & \left[ (1+B) {E'}_{MS} (1+B)^T \right]^{-1}.\end{array}\end{displaymath}](img261.gif) |
(5) |
Changing the integration variable from
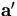 to
to 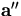 , Eq.A.1 now becomes
, Eq.A.1 now becomes
| ![\begin{displaymath}
\begin{array}
{lll}
P\left({\bf a}_M;{\bf a}\right)
& = & ...
...1} + E_{MS}^{-1} \right) \cdot {\bf a}''
\right] .\end{array}\end{displaymath}](img263.gif) |
(6) |
Notice that the last line is a constant independent of
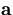 and
and 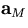 ,which proves that the error matrix including the multiple scattering
has to be
,which proves that the error matrix including the multiple scattering
has to be
| 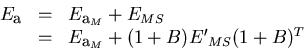 |
(7) |
The derivation of the explicit form of E'MS
is straightforward.
The multiple scattering changes the helix
parameter vector from 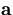 to
to 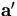 and, when the pivot is chosen to be the point of the multiple scattering,
the tangential vector thereat changes as
and, when the pivot is chosen to be the point of the multiple scattering,
the tangential vector thereat changes as
| 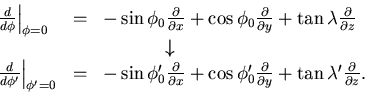 |
(8) |
Then the direction change of the track in space 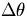 is
given by
is
given by
| 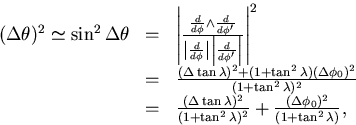 |
(9) |
where 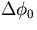 and
and 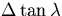 are defined as
components of
are defined as
components of 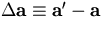 .The above equation determines E'MS through
.The above equation determines E'MS through
| 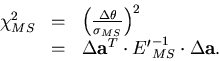 |
(10) |



Next: Measurement Error Matrix at
Up: No Title
Previous: Summary
Keisuke Fujii
12/4/1998
![[*]](foot_motif.gif) .
In the Gaussian approximation valid for small angle multiple scattering,
the probability of getting
.
In the Gaussian approximation valid for small angle multiple scattering,
the probability of getting ![]() to
to ![]() due to multiple scattering there.
We assume here that the track parameter vector of the particle
is measured after the multiple scattering to be
due to multiple scattering there.
We assume here that the track parameter vector of the particle
is measured after the multiple scattering to be ![]() with its error matrix
with its error matrix ![]()
![[*]](foot_motif.gif) .
In the Gaussian approximation valid for small angle multiple scattering,
the probability of getting
.
In the Gaussian approximation valid for small angle multiple scattering,
the probability of getting ![]() when the true track parameter
vector before the multiple scattering is
when the true track parameter
vector before the multiple scattering is ![]() is given by
is given by
![\begin{displaymath}
\begin{array}
{lll}
P\left({\bf a}_M;{\bf a}\right)
& = & ...
...left( {\bf a} - {\bf a}'' \right)
\right) \right],\end{array}\end{displaymath}](img252.gif)
![[*]](foot_motif.gif) N is a normalization factor depending only on
N is a normalization factor depending only on
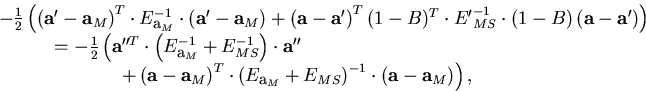
![\begin{displaymath}
\begin{array}
{lll}
E_{MS}^{-1} & \equiv & (1-B)^T {E'}_{MS...
...
& = & \left[ (1+B) {E'}_{MS} (1+B)^T \right]^{-1}.\end{array}\end{displaymath}](img261.gif)
![\begin{displaymath}
\begin{array}
{lll}
P\left({\bf a}_M;{\bf a}\right)
& = & ...
...1} + E_{MS}^{-1} \right) \cdot {\bf a}''
\right] .\end{array}\end{displaymath}](img263.gif)
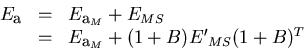
![]() to
to ![]() and, when the pivot is chosen to be the point of the multiple scattering,
the tangential vector thereat changes as
and, when the pivot is chosen to be the point of the multiple scattering,
the tangential vector thereat changes as