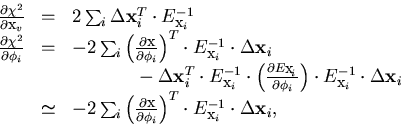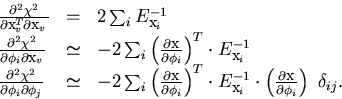Next: Inclusion of Geometrical Constraints
Up: Vertex Fitting
Previous: Vertex Fitting without Error
When error matrices are available, the 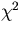 to minimize is defined by
to minimize is defined by
| 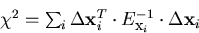 |
(33) |
where
and 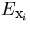 is the position error matrix of
i-th track at the deflection angle
is the position error matrix of
i-th track at the deflection angle 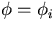 corresponding to the trial vertex
corresponding to the trial vertex 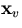 :
The parameter vector to determine by
:
The parameter vector to determine by 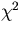 minimization is
where
minimization is
where 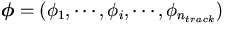 and thus
and thus 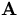 contains
3 + nn<<848>>track parameters.
The
contains
3 + nn<<848>>track parameters.
The 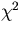 minimization requires the calculations of
the first and the second derivatives of the
minimization requires the calculations of
the first and the second derivatives of the 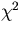 .The first derivatives are calculated as
.The first derivatives are calculated as
| 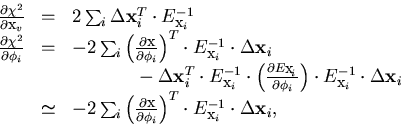 |
(34) |
where in the last step we have ignored the second order term with respect
to the residual vector 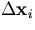 which is a good approximation
near the
which is a good approximation
near the 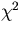 minimum.
From these the second derivatives are readily obtained:
minimum.
From these the second derivatives are readily obtained:
| 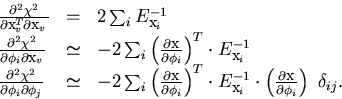 |
(35) |
Notice that when the position error matrices are unity, the problem is
equivalent to the one in the last subsection.
The difference here is the introduction of the error matrices as
metric tensors in the residual space.
Once the derivatives are calculated, all we have to do is to solve
the following linear equation (multi-dimensonal Newton's method)
iteratively:
| 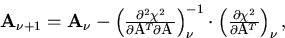 |
(36) |
where the diagonal elements of the second derivative matrix should be
multiplied by some number greater than one when the 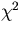 increases
as with the track fitting in Section 2.2.
increases
as with the track fitting in Section 2.2.
When the fit converges, the error matrix for the parameter vector is
obtained to be
| 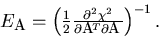 |
(37) |



Next: Inclusion of Geometrical Constraints
Up: Vertex Fitting
Previous: Vertex Fitting without Error
Keisuke Fujii
12/4/1998
![]() to minimize is defined by
to minimize is defined by