Next: Vertex Fitting with Error
Up: Vertex Fitting
Previous: Vertex Fitting
In order to supply an initial vertex position, we first calculate
an approximate vertex position by calculating the intersection
in the xy plane of
two helices arbitrarily chosen from the given set of tracks.
There are two such intersections in general.
We then compares the differences of z coordinates and take the
intersection corresponding to the smaller distance.
The mid-point in the z direction
is our first guess of the common vertex
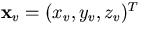 .We approximate the helices to tangential lines at the
points on the helices that are the closest
in the xy plane to the trial vertex position:
.We approximate the helices to tangential lines at the
points on the helices that are the closest
in the xy plane to the trial vertex position:
| 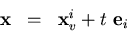 |
(26) |
where
|  |
(27) |
and 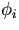 is given by
is given by
| 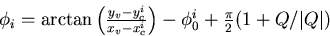 |
(28) |
with (xci,yci) being the center of the i-th helix:
| 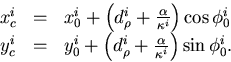 |
(29) |
Then, what to minimize is the sum of the distance squared
of each tangential line from a new trial vertex 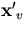 :
:
| 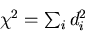 |
(30) |
with
| 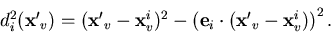 |
(31) |
Notice that the 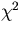 is a quadratic funciton of
is a quadratic funciton of 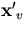 so
that the minimization condition
so
that the minimization condition
| 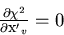 |
(32) |
is a linear equation which can be solved by a single matrix inversion.
The solution 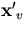 is our improved guess of the common vertex.
We repeat this process until the vertex position converges.
is our improved guess of the common vertex.
We repeat this process until the vertex position converges.



Next: Vertex Fitting with Error
Up: Vertex Fitting
Previous: Vertex Fitting
Keisuke Fujii
12/4/1998
![]() .We approximate the helices to tangential lines at the
points on the helices that are the closest
in the xy plane to the trial vertex position:
.We approximate the helices to tangential lines at the
points on the helices that are the closest
in the xy plane to the trial vertex position: