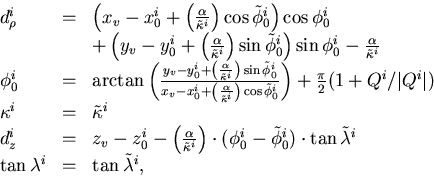Next: High Momentum Limit
Up: Vertex Fitting
Previous: Vertex Fitting with Error
In the last subsection, we tried to determine the common vertex of
given ntrack tracks without touching the track parameter vectors
themselves: these helical tracks do not necessarily pass through the
common vertex.
Here, we require these tracks to originate from a common vertex:
so that i-th track, for instance, can be parametrized as
| 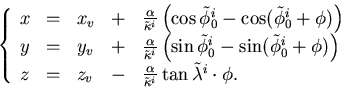 |
(38) |
Notice that, for a given trial vertex 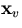 ,
the track parameter vector has now only three components:
since the track has to pass through the pivot
,
the track parameter vector has now only three components:
since the track has to pass through the pivot 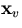 and
therefore
and
therefore 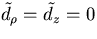 .
.
In order to calculate the 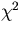 , we need to transform the
pivot of the i-th track from the
trial vertex
, we need to transform the
pivot of the i-th track from the
trial vertex 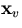 to
the pivot of the corresponding measured track.
This induces the following change of the helix parameters:
to
the pivot of the corresponding measured track.
This induces the following change of the helix parameters:
| 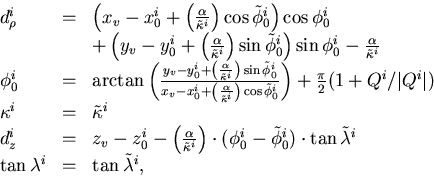 |
(39) |
which gives the helix parameter vector:
to be compared with the corresponding measured track
parameter vector 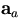 .Thus, we arrive at the
.Thus, we arrive at the 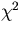 definition:
definition:
| 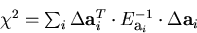 |
(40) |
with
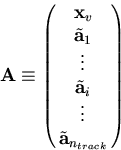
the minimization of which determinies the parameter vector:
containing 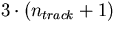 components.
Notice that
the necessary calculations of the first and the second derivatives
of the
components.
Notice that
the necessary calculations of the first and the second derivatives
of the 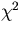 require only the evaluation of the transformation matrix:
and what then follows is the same as with the last subsection.
require only the evaluation of the transformation matrix:
and what then follows is the same as with the last subsection.



Next: High Momentum Limit
Up: Vertex Fitting
Previous: Vertex Fitting with Error
Keisuke Fujii
12/4/1998
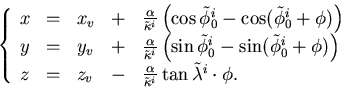
![]() , we need to transform the
pivot of the i-th track from the
trial vertex
, we need to transform the
pivot of the i-th track from the
trial vertex ![]() to
the pivot of the corresponding measured track.
This induces the following change of the helix parameters:
to
the pivot of the corresponding measured track.
This induces the following change of the helix parameters: