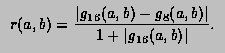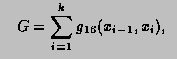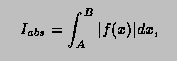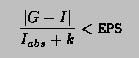TF1

class TF1 : public TFormula, public TAttLine, public TAttFill, public TAttMarker

    public:

                   TF1 TF1(char* name, char* formula, Float_t xmin = 0, Float_t xmax = 1)
                   TF1 TF1(char* name, void* fcn, Float_t xmin = 0, Float_t xmax = 1, Int_t npar = 0)
                   TF1 TF1(char* name, Double_t (*)(Double_t*, Double_t*) fcn, Float_t xmin = 0, Float_t xmax = 1, Int_t npar = 0)
                   TF1 TF1()
                   TF1 TF1(TF1& f1)
          virtual void ~TF1()
          virtual void Browse(TBrowser* b)
               TClass* Class()
          virtual void Copy(TObject& f1)
      virtual Double_t Derivative(Double_t x, Double_t* params = 0, Float_t epsilon = 0)
         virtual Int_t DistancetoPrimitive(Int_t px, Int_t py)
          virtual void Draw(Option_t* option)
          virtual void DrawCopy(Option_t* option)
          virtual void DrawF1(char* formula, Float_t xmin, Float_t xmax, Option_t* option)
          virtual void DrawPanel()
      virtual Double_t Eval(Double_t x, Double_t y = 0, Double_t z = 0)
      virtual Double_t EvalPar(Double_t* x, Double_t* params = 0)
          virtual void ExecuteEvent(Int_t event, Int_t px, Int_t py)
              Double_t GetChisquare()
                 TH1F* GetHistogram()
          TMethodCall* GetMethodCall()
                 Int_t GetNpx()
                 Int_t GetNumberFitPoints()
              TObject* GetParent()
              Double_t GetParError(Int_t ipar)
          virtual void GetParLimits(Int_t ipar, Double_t& parmin, Double_t& parmax)
      virtual Double_t GetRandom()
          virtual void GetRange(Float_t& xmin, Float_t& ymin, Float_t& zmin, Float_t& xmax, Float_t& ymax, Float_t& zmax)
          virtual void GetRange(Float_t& xmin, Float_t& ymin, Float_t& xmax, Float_t& ymax)
          virtual void GetRange(Float_t& xmin, Float_t& xmax)
      virtual Double_t GetSave(Double_t* x)
               Float_t GetXmax()
               Float_t GetXmin()
          virtual void InitArgs(Double_t* x, Double_t* params)
      virtual Double_t Integral(Float_t a, Float_t b, Double_t* params = 0, Float_t epsilon = 0.000001)
       virtual TClass* IsA()
         virtual Int_t LocateBinary(Double_t value, Double_t* array, Int_t nbins)
          virtual void Paint(Option_t* option)
          virtual void Print(Option_t* option)
          virtual void Save(Float_t xmin, Float_t xmax)
          virtual void SavePrimitive(ofstream& out, Option_t* option)
          virtual void SetChisquare(Double_t chi2)
          virtual void SetMaximum(Float_t maximum = -1111)
          virtual void SetMinimum(Float_t minimum = -1111)
          virtual void SetNpx(Int_t npx = 100)
          virtual void SetNumberFitPoints(Int_t npfits)
          virtual void SetParent(TObject* p = 0)
          virtual void SetParError(Int_t ipar, Double_t error)
          virtual void SetParLimits(Int_t ipar, Double_t parmin, Double_t parmax)
          virtual void SetRange(Float_t xmin, Float_t ymin, Float_t zmin, Float_t xmax, Float_t ymax, Float_t zmax)
          virtual void SetRange(Float_t xmin, Float_t ymin, Float_t xmax, Float_t ymax)
          virtual void SetRange(Float_t xmin, Float_t xmax)
          virtual void ShowMembers(TMemberInspector& insp, char* parent)
          virtual void Streamer(TBuffer& b)

  Data Members

    protected:

                                  Float_t fXmin        Lower bounds for the range
                                  Float_t fXmax        Upper bounds for the range
                                    Int_t fNpx         Number of points used for the graphical representation
                                    Int_t fType        (=0 for standard functions, 1 if pointer to function)
                                    Int_t fNpfits      Number of points used in the fit
                                    Int_t fNsave       Number of points used to fill array fSave
                                 Double_t fChisquare   Function fit chisquare
                                Double_t* fIntegral    Integral of function binned on fNpx bins
                                Double_t* fParErrors   Array of errors of the fNpar parameters
                                Double_t* fParMin      Array of lower limits of the fNpar parameters
                                Double_t* fParMax      Array of upper limits of the fNpar parameters
                                Double_t* fSave        Array of fNsave function values
                                 TObject* fParent      Parent object hooking this function (if one)
                                    TH1F* fHistogram   Pointer to histogram used for visualisation
                                  Float_t fMaximum     Maximum value for plotting
                                  Float_t fMinimum     Minimum value for plotting
                             TMethodCall* fMethodCall  Pointer to MethodCall in case of interpreted function
      Double_t (*)(Double_t*, Double_t*)* fFunction    Pointer to function

See also

TF2

Class Description

 a TF1 object is a 1-Dim function defined between a lower and upper limit.
 The function may be a simple function (see TFormula) or a precompiled
 user function.
 The function may have associated parameters.
 TF1 graphics function is via the TH1/TGraph drawing functions.

  The following types of functions can be created:
    A- Expression using variable x and no parameters
    B- Expression using variable x with parameters
    C- A general C function with parameters

      Example of a function of type A

   TF1 *f1 = new TF1("f1","sin(x)/x",0,10);
   f1->Draw();

/*

*/


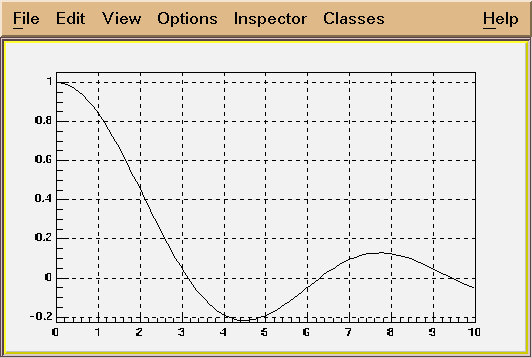      Example of a function of type B
   TF1 *f1 = new TF1("f1","[0]x*sin([1]*x",-3,3);
    This creates a function of variable x with 2 parameters.
    The parameters must be initialized via:
      f1->SetParameter(0,value_first_parameter);
      f1->SetParameter(1,value_second_parameter);
    Parameters may be given a name:
      f1->SetParName(0,"Constant");

     Example of function of type C
   Consider the macro myfunc.C below
-------------macro myfunc.C-----------------------------
Double_t myfunction(Double_t *x, Double_t *par)
{
   Float_t xx =x[0];
   Double_t f = TMath::Abs(par[0]*sin(par[1]*xx)/xx);
   return f;
}
void myfunc()
{
   TF1 *f1 = new TF1("myfunc",myfunction,0,10,2);
   f1->SetParameters(2,1);
   f1->SetParNames("constant","coefficient");
   f1->Draw();
}
void myfit()
{
   TH1F *h1=new TH1F("h1","test",100,0,10);
   h1->FillRandom("myfunc",20000);
   TF1 *f1=gROOT->GetFunction("myfunc");
   f1->SetParameters(800,1);
   h1.Fit("myfunc");
}
--------end of macro myfunc.C---------------------------------

 In an interactive session you can do:
   Root > .L myfunc.C
   Root > myfunc();
   Root > myfit();

*-*-*-*-*-*-*-*-*-*-*F1 default constructor*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
*-*                  ======================

*-*-*-*-*-*-*F1 constructor using a formula definition*-*-*-*-*-*-*-*-*-*-*
*-*          =========================================
*-*
*-*  See TFormula constructor for explanation of the formula syntax.
*-*
*-*  Creates a function of type A or B between xmin and xmax
*-*
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*

*-*-*-*-*-*-*F1 constructor using pointer to an interpreted function*-*-*-*
*-*          =======================================================
*-*
*-*  See TFormula constructor for explanation of the formula syntax.
*-*
*-*  Creates a function of type C between xmin and xmax.
*-*  The function is defined with npar parameters
*-*  fcn must be a function of type:
*-*     Double_t fcn(Double_t *x, Double_t *params)
*-*
*-*  This constructor is called for functions of type C by CINT.
*-*
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*

*-*-*-*-*-*-*F1 constructor using a pointer to real function*-*-*-*-*-*-*-*
*-*          ===============================================
*-*
*-*   npar is the number of free parameters used by the function
*-*
*-*   This constructor creates a function of type C when invoked
*-*   with the normal C++ compiler.
*-*
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*

*-*-*-*-*-*-*-*-*-*-*F1 default destructor*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
*-*                  =====================

*-*-*-*-*-*-*-*-*-*-*Copy this F1 to a new F1*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
*-*                  ========================

*-*-*-*-*-*-*-*-*Return derivative of function at point x*-*-*-*-*-*-*-*

    The derivative is computed by computing the value of the function
   at point x-epsilon and point x+epsilon.
   if params is NULL, use the current values of parameters

*-*-*-*-*-*-*-*-*-*-*Compute distance from point px,py to a function*-*-*-*-*
*-*                  ===============================================
*-*  Compute the closest distance of approach from point px,py to this function.
*-*  The distance is computed in pixels units.
*-*
*-*  Algorithm:
*-*
*-*
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*

*-*-*-*-*-*-*-*-*-*-*Draw this function with its current attributes*-*-*-*-*
*-*                  ==============================================
*-*
*-* Possible option values are:
*-*   "SAME"  superimpose on top of existing picture
*-*   "L"     connect all computed points with a straight line
*-*   "C"     connect all computed points with a smooth curve.
*-*
*-* Note that the default value is "L". Therefore to draw on top
*-* of an existing picture, specify option "LSAME"
*-*
*-* NB. You must use DrawCopy if you want to draw several times the same
*-*     function in the current canvas.
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*

*-*-*-*-*-*-*-*Draw a copy of this function with its current attributes*-*-*
*-*            ========================================================
*-*
*-*  This function MUST be used instead of Draw when you want to draw
*-*  the same function with different parameters settings in the same canvas.
*-*
*-* Possible option values are:
*-*   "SAME"  superimpose on top of existing picture
*-*   "L"     connect all computed points with a straight line
*-*   "C"     connect all computed points with a smooth curve.
*-*
*-* Note that the default value is "L". Therefore to draw on top
*-* of an existing picture, specify option "LSAME"
*-*
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*

*-*-*-*-*-*-*-*-*-*Draw formula between xmin and xmax*-*-*-*-*-*-*-*-*-*-*-*
*-*                ==================================
*-*

*-*-*-*-*-*-*Display a panel with all function drawing options*-*-*-*-*-*
*-*          =================================================
*-*
*-*   See class TDrawPanelHist for example

*-*-*-*-*-*-*-*-*-*-*Evaluate this formula*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
*-*                  =====================
*-*
*-*   Computes the value of this function (general case for a 3-d function)
*-*   at point x,y,z.
*-*   For a 1-d function give y=0 and z=0
*-*   The current value of variables x,y,z is passed through x, y and z.
*-*   The parameters used will be the ones in the array params if params is given
*-*    otherwise parameters will be taken from the stored data members fParams
*-*
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*

*-*-*-*-*-*Evaluate function with given coordinates and parameters*-*-*-*-*-*
*-*        =======================================================
*-*
      Compute the value of this function at point defined by array x
      and current values of parameters in array params.
      If argument params is omitted or equal 0, the internal values
      of parameters (array fParams) will be used instead.
      For a 1-D function only x[0] must be given.
      In case of a multi-dimemsional function, the arrays x must be
      filled with the corresponding number of dimensions.

   WARNING. In case of an interpreted function (fType=2), it is the
   user's responsability to initialize the parameters via InitArgs
   before calling this function.
   InitArgs should be called at least once to specify the addresses
   of the arguments x and params.
   InitArgs should be called everytime these addresses change.

*-*-*-*-*-*-*-*-*-*-*Execute action corresponding to one event*-*-*-*
*-*                  =========================================
*-*  This member function is called when a F1 is clicked with the locator
*-*
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*

*-*-*-*-*-*Return limits for parameter ipar*-*-*-*
*-*        ================================

*-*-*-*-*-*Return a random number following this function shape*-*-*-*-*-*-*
*-*        ====================================================
*-*
*-*   The distribution contained in the function fname (TF1) is integrated
*-*   over the channel contents.
*-*   It is normalized to 1.
*-*   Getting one random number implies:
*-*     - Generating a random number between 0 and 1 (say r1)
*-*     - Look in which bin in the normalized integral r1 corresponds to
*-*     - make a linear interpolation in the returned bin
*-*
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-**-*-*-*-*-*-*-*

*-*-*-*-*-*-*-*-*-*-*Return range of a 1-D function*-*-*-*-*-*-*-*-*-*-*-*
*-*                  ==============================

*-*-*-*-*-*-*-*-*-*-*Return range of a 2-D function*-*-*-*-*-*-*-*-*-*-*-*-*
*-*                  ==============================

*-*-*-*-*-*-*-*-*-*-*Return range of function*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
*-*                  ========================

 Get value corresponding to X in array of fSave values

*-*-*-*-*-*-*-*-*-*-*Initialize parameters addresses*-*-*-*-*-*-*-*-*-*-*-*
*-*                  ===============================

*-*-*-*-*-*-*-*-*Return Integral of function between a and b*-*-*-*-*-*-*-*

   based on original CERNLIB routine DGAUSS by Sigfried Kolbig
   converted to C++ by Rene Brun


/*



This function computes,
to an attempted specified accuracy, the value of the integral
 
  


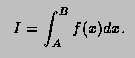
Usage:

In any arithmetic expression, this function
has the approximate value of the integral I.

a,b
End-points of integration interval. Note that B
may be less than A.
params
Array of function parameters. If 0, use current parameters.
epsilon
Accuracy parameter (see Accuracy).


Method:

For any interval [a,b] we define 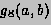   and 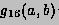   to be the
8-point and 16-point Gaussian quadrature approximations to
     
  

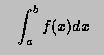
and define
  

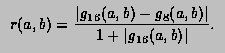
Then,
  


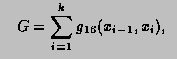
where, starting with 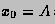   and finishing with   ,
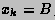the subdivision points 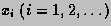   are given by
  

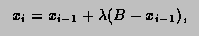
with 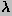   equal to the first member of the sequence
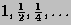   for which
  .
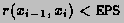If, at any stage in the process of subdivision, the ratio
  
  

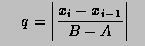
is so small that 1+0.005q is indistinguishable from 1 to
machine accuracy, an error exit occurs with the function value
set equal to zero.

Accuracy:

Unless there is severe cancellation of positive and negative
values of f(x) over the interval [A,B], the argument EPS
may be considered as specifying a bound on the relative error of
I in the case  |I|>1, and a bound on the absolute error in
the case |I|<1. More precisely, if k is the number of sub-intervals
contributing to the approximation (see Method), and if
  

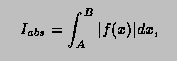
then the relation
  

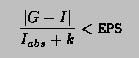
will nearly always be true, provided the routine terminates
without printing an error message. For functions
f having no singularities in the closed interval [A,B]
the accuracy will usually be much higher than this.

Error handling:

The requested accuracy cannot be
obtained (see Method).
The function value is set equal to zero.

Notes:

Values of the function f(x) at the interval end-points
A and B are not required. The subprogram may therefore
be used when these values are undefined.


*/

---------------------------------------------------------------

*-*-*-*-*-*-*Binary search in an array of nbins to locate value*-*-*-*-*-*-*
*-*          ==================================================
*-*  array is supposed  to be sorted prior to this call.
*-*  If match is found, function returns position of element.
*-*  If no match found, function gives nearest element smaller than value.
*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*

*-*-*-*-*-*-*-*-*-*-*Paint this function with its current attributes*-*-*-*-*
*-*                  ===============================================

*-*-*-*-*-*-*-*-*-*-*Dump this function with its attributes*-*-*-*-*-*-*-*-*-*
*-*                  ==================================

 Save values of function in array fSave

 Save primitive as a C++ statement(s) on output stream out

*-*-*-*-*-*-*-*Set the number of points used to draw the function*-*-*-*-*-*
*-*            ==================================================

*-*-*-*-*-*Set limits for parameter ipar*-*-*-*
*-*        =============================
     The specified limits will be used in a fit operation
     when the option "B" is specified (Bounds).

*-*-*-*-*-*Initialize the upper and lower bounds to draw the function*-*-*-*
*-*        ==========================================================
     The function range is also used in an histogram fit operation
     when the option "R" is specified.

*-*-*-*-*-*-*-*-*Stream a class object*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
*-*              =========================================

Inline Functions

            Double_t GetChisquare()
               TH1F* GetHistogram()
               Int_t GetNpx()
        TMethodCall* GetMethodCall()
               Int_t GetNumberFitPoints()
            TObject* GetParent()
            Double_t GetParError(Int_t ipar)
             Float_t GetXmin()
             Float_t GetXmax()
                void SetChisquare(Double_t chi2)
                void SetMaximum(Float_t maximum = -1111)
                void SetMinimum(Float_t minimum = -1111)
                void SetNumberFitPoints(Int_t npfits)
                void SetParError(Int_t ipar, Double_t error)
                void SetParent(TObject* p = 0)
                void SetRange(Float_t xmin, Float_t ymin, Float_t xmax, Float_t ymax)
                void SetRange(Float_t xmin, Float_t ymin, Float_t zmin, Float_t xmax, Float_t ymax, Float_t zmax)
             TClass* Class()
             TClass* IsA()
                void ShowMembers(TMemberInspector& insp, char* parent)