




Next: Quantum Electrodynamics Involving a
Up: Laser
Previous: Laser Geometry
When the parameter NPH=0 is specified in LASERQED command,
the formulas of linear Compton scattering are used.
Let us define the following variables in the rest frame of the initial
electron:
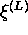 ,
,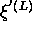
- Photon Stokes parameters
before and after collision as defined in[3](page 361).

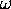 ,
,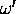
- Initial (laser) and final energies of the photon.
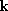 ,
,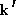
- Initial (laser) and final momenta of the photon.
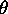 ,
, 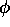
- Polar and azimuthal scattering angle of the photon.
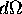
- Solid angle
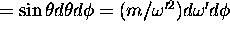 .
.
The range of 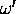 is given by
is given by
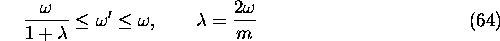
The Compton relation is

The crosssection is given by eq(87.22) in [3].
 :
:
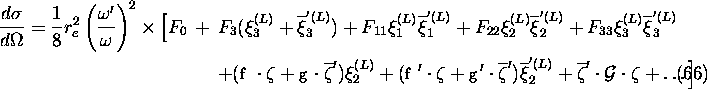
See Sec.5.2.2 for the meaning of the bars on 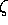 and
and
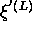 . The omitted terms are products of three and four among
. The omitted terms are products of three and four among 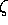 ,
,
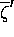 ,
, 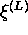 , and
, and 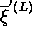 .
(Actually, we need the terms
.
(Actually, we need the terms 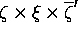 and
and
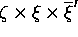 but they are not found in literature.)
The functions introduced in the above expression are:
but they are not found in literature.)
The functions introduced in the above expression are:
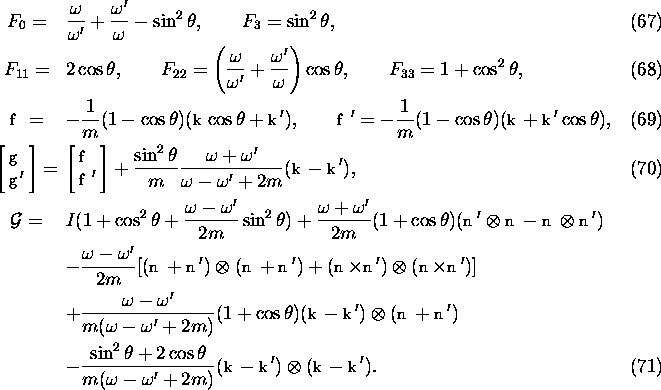
These formulas are used in their exact forms in CAIN.
Summation over the final polarization and the azimuthal angle  gives the differential crosssection with respect to the final photon energy
gives the differential crosssection with respect to the final photon energy
 . Introducing the variables
. Introducing the variables 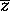 inplace of
inplace of 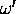 by
by
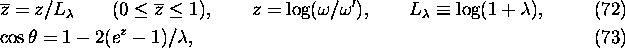
we write the differential crossection as

where
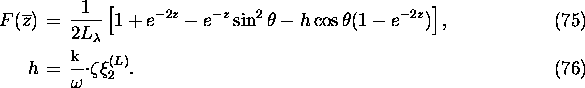
Note that 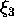 does not appear here because it is based on the scattering plane
and, therefore, disappears after integration over the azimuthal angle.
The function
does not appear here because it is based on the scattering plane
and, therefore, disappears after integration over the azimuthal angle.
The function 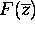 satisfies
satisfies 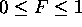 for any
for any 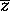 and
and 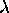 and is O(1) except when h is close to +1 and
and is O(1) except when h is close to +1 and 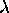 is extremely large.
The Function
is extremely large.
The Function 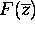 is plotted in Fig.5.
is plotted in Fig.5.
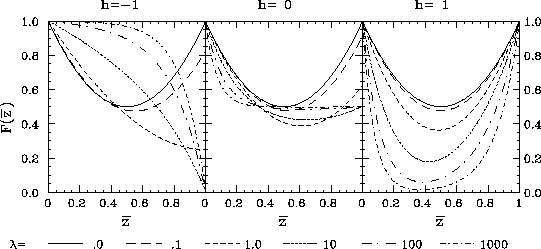
Figure 5: Function 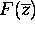 for
for 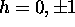 for various values of
for various values of 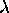
The total crosssection for given initial momenta and polarizations is given by

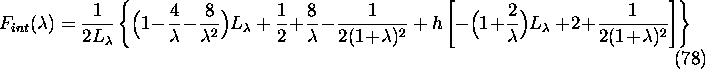
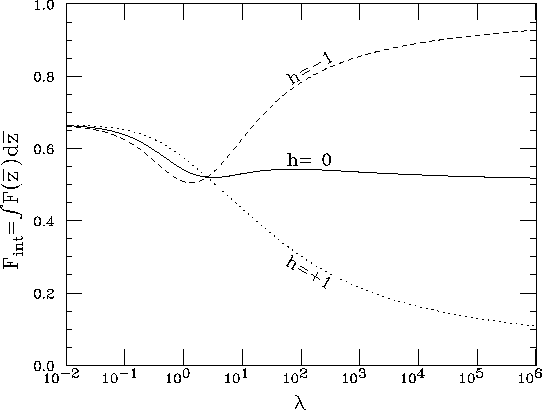
Figure 6: Function 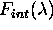 for
for 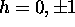 as a function of
as a function of 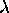 .
.
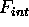 is less than unity and is O(1) unless h is close to +1 and
is less than unity and is O(1) unless h is close to +1 and
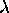 is extremely large.
is extremely large.
Let us briefly describe the algorithm of event generation.
- Compute the total event rate
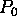 in the given time interval using
in the given time interval using 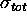 without the factor
without the factor 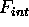 . Since
. Since 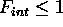 , this is an over estimation
of the rate. If
, this is an over estimation
of the rate. If 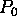 is too large, divide the time interval by an integer N
and repeat the following procedure N times.
is too large, divide the time interval by an integer N
and repeat the following procedure N times.
- Generate a random number
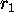 uniform in (0,1). Reject if
uniform in (0,1). Reject if 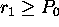 .
.
- Compute
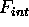 and multiply it to
and multiply it to 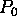 . Reject if still
. Reject if still 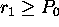 .
Otherwise accept. Note that the Lorentz transformation of
.
Otherwise accept. Note that the Lorentz transformation of
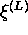 is not
needed for the computation of h because
is not
needed for the computation of h because
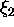 is Lorentz invariant. Also note that input
is Lorentz invariant. Also note that input 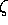 is defined
already in the rest frame of electron. Only the Lorentz transformation of
is defined
already in the rest frame of electron. Only the Lorentz transformation of 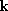 is needed.
is needed.
- Generate two random numbers
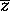 and
and 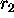 in (0,1). Repeat this step
until
in (0,1). Repeat this step
until 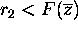 is satisfied. Once or twice repetition is
normally enough unless h is close to +1 and
is satisfied. Once or twice repetition is
normally enough unless h is close to +1 and 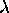 is very large.
is very large.
- Compute
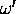 from
from 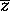 . Generate the azimuthal angle,
compute the final polarization if needed, and go back to the
laboratory frame. In this step many Lorentz transformations are needed.
. Generate the azimuthal angle,
compute the final polarization if needed, and go back to the
laboratory frame. In this step many Lorentz transformations are needed.





Next: Quantum Electrodynamics Involving a
Up: Laser
Previous: Laser Geometry
Toshiaki Tauchi
Thu Dec 3 17:27:26 JST 1998
![]() gives the differential crosssection with respect to the final photon energy
gives the differential crosssection with respect to the final photon energy
![]() . Introducing the variables
. Introducing the variables ![]() inplace of
inplace of ![]() by
by
![]()
![]()
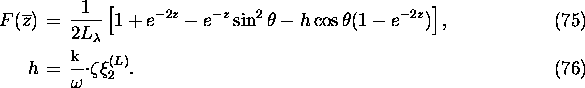
![]() does not appear here because it is based on the scattering plane
and, therefore, disappears after integration over the azimuthal angle.
The function
does not appear here because it is based on the scattering plane
and, therefore, disappears after integration over the azimuthal angle.
The function ![]() satisfies
satisfies ![]() for any
for any ![]() and
and ![]() and is O(1) except when h is close to +1 and
and is O(1) except when h is close to +1 and ![]() is extremely large.
The Function
is extremely large.
The Function ![]() is plotted in Fig.5.
is plotted in Fig.5.

![]() for
for ![]() for various values of
for various values of ![]()
![]()
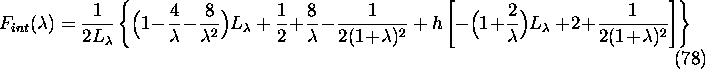

![]() for
for ![]() as a function of
as a function of ![]() .
.
![]() is less than unity and is O(1) unless h is close to +1 and
is less than unity and is O(1) unless h is close to +1 and
![]() is extremely large.
is extremely large.