where
When the laser field is strong, the simple formulas
of Compton/Breit-Wheeler can nolonger be used. The laser strength is
characterized by the parameter
![]()
where ![]() is the laser wavelength
is the laser wavelength ![]() in meter,
m the electron rest mass in eV/
in meter,
m the electron rest mass in eV/![]() ,
c the velocity of light in m/s,
,
c the velocity of light in m/s, ![]() ,
and P the power density in Watt/m
,
and P the power density in Watt/m![]() .
When
.
When ![]() , the simple formas are enough but as
, the simple formas are enough but as ![]() becomes large,
the probability of absorbing more than one photon in the laser field
cannot be ignored. When
becomes large,
the probability of absorbing more than one photon in the laser field
cannot be ignored. When ![]() ,
the constant-field approximation
,
the constant-field approximation![]() becomes good.
If
becomes good.
If ![]() , the expansion in terms of the number of absorbed photons, n,
shows good convergence. The expansion takes a relatively simple form
when the laser is circularly polarized by 100%. The present version
accepts such case only.
, the expansion in terms of the number of absorbed photons, n,
shows good convergence. The expansion takes a relatively simple form
when the laser is circularly polarized by 100%. The present version
accepts such case only.
In the case of the nonlinear Compton process
![]() ,
the number of emitted photons per unit time
can be expanded in the form
,
the number of emitted photons per unit time
can be expanded in the form![]()
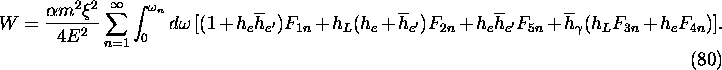
The formula for the nonlinear Breit-Wheeler process
![]() can be written in a similar form.
The total number of pair electrons per unit time summed over the positron
polarization is
can be written in a similar form.
The total number of pair electrons per unit time summed over the positron
polarization is
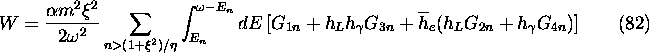
When NPH![]() is specified in LASERQED command,
the above formulas are used with the terms upto n=NPH.
See Sec.A for the algorithm of the event generation.
is specified in LASERQED command,
the above formulas are used with the terms upto n=NPH.
See Sec.A for the algorithm of the event generation.