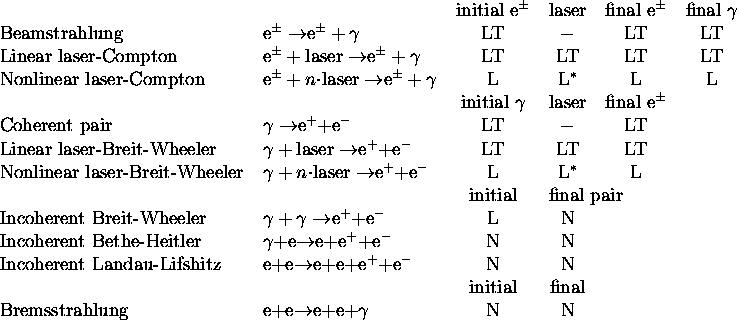where
where
In most applications, one is interested in the helicity states. Therefore, one possible way of expressing the electron/positron spin is to store the information whether each macro-particle is in the helicity h=+1 state of -1 state. The unpolarized state is represented by an equal number of macro-particles with h=+1 and -1. The spin may flip at the interactions such as laser-Compton scattering and beamstrahlung.
However, this simple way cannot be applied to our case because, for example, a pure transverse polarization may become longitudinal during the precession in a magnetic field (beam-beam field or external field). In order to include such classical precession effects, the phase relation between the up and down components of the spinor is important.
This problem can be solved by using the density matrix. Let us express
an electron(positron) state by a two-component spinor ![]() .
The 2
.
The 2![]() 2 density matrix
2 density matrix ![]() is defined as
is defined as
![]()
where ![]() denotes the Hermitian conjugate and
denotes the Hermitian conjugate and ![]() is the average over a
particle ensemble.
Since
is the average over a
particle ensemble.
Since ![]() is Hermitian and its trace is unity by normalization,
is Hermitian and its trace is unity by normalization,
![]() can be written as
can be written as
![]()
where ![]() is the Pauli matrices. The 3-vector
is the Pauli matrices. The 3-vector ![]() is
called polarization vector .
is
called polarization vector .
In the case of pure states, ![]() can be represented by a superposition
of spin up(down) states
can be represented by a superposition
of spin up(down) states ![]() :
:
![]()
With the standard
representation of the Pauli matrices
![]()
![]() can be written as
can be written as
![]()
and its length is unity: ![]() . CAIN allows
. CAIN allows
![]() so that each macro-particle is in a mixed state,
representing an ensemble of particles having almost the same energy-momentum
and space-time coordinate.
so that each macro-particle is in a mixed state,
representing an ensemble of particles having almost the same energy-momentum
and space-time coordinate.
If one observes
the particle spin with the quantization axis ![]() (
(![]() ),
the probability to be found in the spin
),
the probability to be found in the spin ![]() state is given by
state is given by
![]() .
.
The polarization vector ![]() obeys the Thomas-BMT equation
(33) in the absense of quantum phenomena.
obeys the Thomas-BMT equation
(33) in the absense of quantum phenomena.
1ex
A similar way is used for photon polarization, too. The polarization
vector (3-vector) ![]() (normalized as
(normalized as ![]() )
is orthogonal to the photon momentum
)
is orthogonal to the photon momentum ![]() .
It can be represented by the components along two unit vectors
.
It can be represented by the components along two unit vectors
![]() and
and ![]() perpendicular to
perpendicular to ![]() .
The three vectors (
.
The three vectors (![]() ,
, ![]() ,
,
![]() ) form a right-handed orthonormal basis.
The density matrix is defined as
) form a right-handed orthonormal basis.
The density matrix is defined as
![]()
This is Hermitian with unit trace as in the case of electron density matrix so that
it can be written as
![]()
The 3-vector ![]() is called the Stokes parameter. In the standard
representation of the Pauli matrices,
the three components of
is called the Stokes parameter. In the standard
representation of the Pauli matrices,
the three components of ![]() have the meaning
have the meaning
1ex
In any process involving polarizations, the transition rate (or crosssection)
is given by multiplying the density matrices and by taking the trace. Therefore,
the expressions for the rates are bilinear forms for each polarization vector,
initial/final electron/positron or photon. The final polarization needs
some comments. The transition rate is written in general as
![]()
where ![]() represents the final energy-momentum variables
and w and
represents the final energy-momentum variables
and w and ![]() are functions of
are functions of ![]() . The vector
. The vector ![]() itself is not the final polarization. Its direction is defined by the setup
of the detectors. What the term
itself is not the final polarization. Its direction is defined by the setup
of the detectors. What the term ![]() means is that,
if one observes the spin direction
means is that,
if one observes the spin direction ![]() (
(![]() ),
the probability to be found in the state
),
the probability to be found in the state ![]() is given by
is given by
![]() .
.
The final energy-momentum
distribution is determined by ![]() . For given
. For given ![]() , the final
polarization vector is (see [3], page 254)
, the final
polarization vector is (see [3], page 254)
![]()
Now, consider a process involving initial and final electrons, summing over
other possible particles. The transition rate is written as
![]()
where the subscripts i and f denote initial and final variables,
![]() represents transpose, and H is a 3
represents transpose, and H is a 3![]() 3 matrix.
For given
3 matrix.
For given ![]() , the final energy-momentum distribution is
determined by
, the final energy-momentum distribution is
determined by ![]() . In a Monte Carlo algorithm,
. In a Monte Carlo algorithm,
![]() is decided by using random numbers according to
is decided by using random numbers according to
![]() . Once
. Once ![]() is decided, the final
polarization is definitely (without using random numbers) given by
is decided, the final
polarization is definitely (without using random numbers) given by
![]()
This expression does not satisfy ![]() . If one does not
allow a macro-particle in a mixed state, one has to choose a pure state
by using random numbers.
. If one does not
allow a macro-particle in a mixed state, one has to choose a pure state
by using random numbers.
The macro-particles which did not make transition must carefully be treated.
One might say their final polarization is equal to ![]() but this is not correct because of the selection effect
due to the term
but this is not correct because of the selection effect
due to the term ![]() .
.
The probability that a transion does not occur in a time interval ![]() is
is
![]() ,
where the underlines indicates quantities integrated over the whole
kinetic range of
,
where the underlines indicates quantities integrated over the whole
kinetic range of ![]() .
Consider an ensemble (one macro-particle) of N (real) particles
having the polarization vector
.
Consider an ensemble (one macro-particle) of N (real) particles
having the polarization vector ![]() (
(![]() ).
Each of these is a unit vector
).
Each of these is a unit vector ![]() and
the average over the ensemble is
and
the average over the ensemble is ![]() .
.
Let us arbitrarily take the quatization axis ![]() . The probability
in the state
. The probability
in the state ![]() is
is ![]() and the non-transition probability is
and the non-transition probability is
![]() .
Therefore, the sum of the final polarization along
.
Therefore, the sum of the final polarization along ![]() over the ensemble
is
over the ensemble
is
![]()
The axis ![]() is arbitrary. Therefore, the sum of the final polarization
vector is given by the above expression with
is arbitrary. Therefore, the sum of the final polarization
vector is given by the above expression with ![]() taken away. The total number
of particles without transition is
taken away. The total number
of particles without transition is
![]() .
Thus, the final polarization vector is
.
Thus, the final polarization vector is
![]()
The average final polarization over the whole ensemble, with and without transition,
is then given by
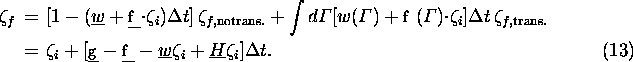
If one can ignore the change of energy-momentum during the transition,
the evolution of the polarization is described by the differential equation
![]()
3ex The present version of CAIN does not include all the polarization effects. The following table shows what effects are included. In any case, the correlation of polarization between final particles is not taken into account.