where C is an appropriate normalization factor, and
The integration is done by introducing the time step size ![]() ,
longitudinal slice width
,
longitudinal slice width ![]() , transverse mesh size
, transverse mesh size
![]() and
and ![]() . Summing the number of particles in each bin,
the luminosity is given by
. Summing the number of particles in each bin,
the luminosity is given by
![]()
where C is an appropriate normalization factor, and
![]() is the number of particles of the beam j
in the bin
is the number of particles of the beam j
in the bin ![]() . A problem is how to determine the
transverse size
of the bin (
. A problem is how to determine the
transverse size
of the bin (![]() and
and ![]() is mainly
determined by the dynamics -- they are actually specified by the user).
If the bin is too large, detail of the distribution is lost, whereas
if too small, statistical error becomes large because each bin will
contain only a small number of macro-particles. CAIN adopts the
following way.
is mainly
determined by the dynamics -- they are actually specified by the user).
If the bin is too large, detail of the distribution is lost, whereas
if too small, statistical error becomes large because each bin will
contain only a small number of macro-particles. CAIN adopts the
following way.
At first, determine the size of the whole transverse region
![]() such that most particles are contained there. Then,
divide this region into as many bins
such that most particles are contained there. Then,
divide this region into as many bins ![]() as allowed by the storage requirement (n must be a power of 2.
CAIN uses n=128.), and count the number of particles in each bin
for both beams
as allowed by the storage requirement (n must be a power of 2.
CAIN uses n=128.), and count the number of particles in each bin
for both beams ![]() (
(![]() ).
).
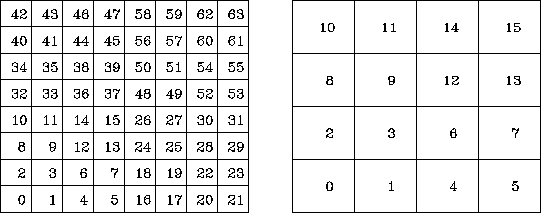
Figure 2: Bin numbering for luminosity integration.
Example with n=8 and the double-sized bin n=4.
If the number of macro-particles in any of the neighbouring 4 bins are
less than some number ![]() (CAIN adopts 5) for both beams, then sum
these numbers and put the sum into a larger bin
(CAIN adopts 5) for both beams, then sum
these numbers and put the sum into a larger bin ![]() .
(For the example in Fig.2,
the sum of the bins 12, 13, 14, and 15 in the figure on the left
corresponds to the bin 3 on the right.)
Otherwise,
add
.
(For the example in Fig.2,
the sum of the bins 12, 13, 14, and 15 in the figure on the left
corresponds to the bin 3 on the right.)
Otherwise,
add ![]() into the luminosity sum. This doubling of
the bin size is repeated so long as
into the luminosity sum. This doubling of
the bin size is repeated so long as ![]() .
In order to make this algorithm efficient, the bin numbering system is
a little complicated. Instead of using two indices
.
In order to make this algorithm efficient, the bin numbering system is
a little complicated. Instead of using two indices ![]() ,
the bins are numbered as in Fig.2. With this numbering,
the sum of neighbouring bins can be simply written as
,
the bins are numbered as in Fig.2. With this numbering,
the sum of neighbouring bins can be simply written as
![]()
where ![]() is the number of particles in the k-th bin
(
is the number of particles in the k-th bin
(![]() ) in
) in ![]() bin system.
bin system.