The calculation of the beam electric field is done in the following way.
First, cut the right(left)-going particles into longitudinal slices
(the width ![]() is defined by the parameter Smesh).
Within each slice
the following Poisson equation is solved.
is defined by the parameter Smesh).
Within each slice
the following Poisson equation is solved.
![]()
where m is the electron mass in units of eV/c![]() ,
, ![]() the
classical electron radius in meters,
the
classical electron radius in meters,
![]() is the charge (divided by the elementary charge)
per unit transverse area, then
is the charge (divided by the elementary charge)
per unit transverse area, then ![]() is given in units of V/m.
is given in units of V/m.
For each slice and for each of right- and left going beams,
a region ![]() is selected,
where
is selected,
where ![]() is the center-of-mass and
is the center-of-mass and ![]() is the
width determined by the input parameters. The field created by the
particles outside this region is ignored. Let us name this region [O].
is the
width determined by the input parameters. The field created by the
particles outside this region is ignored. Let us name this region [O].
In the region [O], the Poisson equation
is solved using the FFT.
Eq.(42) can formally be solved as
![]()
Divide this region by ![]() grid.
Within each cell (i,j) (
grid.
Within each cell (i,j) (![]() ,
, ![]() ), the
the density
), the
the density ![]() is approximated by
is approximated by
![]() , where
, where ![]() ,
, ![]() ,
and
,
and ![]() is the total charge in the cell:
is the total charge in the cell:
![]()
where (![]() ) is the cell center coordinate.
Then, eq.(43) becomes a sum over the cells.
) is the cell center coordinate.
Then, eq.(43) becomes a sum over the cells.
![]()
The kernel matrix ![]() has to be calculated by taking average
over the source cell:
has to be calculated by taking average
over the source cell:
![]()
This averaging is important when ![]() is far from unity.
The convolution in eq.(45) can be done efficiently by using FFT.
is far from unity.
The convolution in eq.(45) can be done efficiently by using FFT.
However, if we apply FFT for the finite region ![]() instead
of the infinite region in eq.(43), we would be assuming
a periodic charge distribution, i.e., the charge
distribution in
instead
of the infinite region in eq.(43), we would be assuming
a periodic charge distribution, i.e., the charge
distribution in ![]() is infinitely repeated.
To avoid this problem, we use the following trick.
First double the region to
is infinitely repeated.
To avoid this problem, we use the following trick.
First double the region to ![]() by padding zero in the
extended region and carry out FFT. This still means a periodic
charge distribution as depicted in Fig.3.
However, if we use the kernel matrix with zero padded
in the
extended region (
by padding zero in the
extended region and carry out FFT. This still means a periodic
charge distribution as depicted in Fig.3.
However, if we use the kernel matrix with zero padded
in the
extended region (![]() if
if ![]() or
or ![]() ),
the field due to the ghost charges will never
reach the real charge region because their horizontal(vertical) distance is
larger than
),
the field due to the ghost charges will never
reach the real charge region because their horizontal(vertical) distance is
larger than ![]() (
(![]() ). Thus, the potential
). Thus, the potential ![]() in the region
in the region
![]() is calculated correctly although incorrect in the extended
region.
is calculated correctly although incorrect in the extended
region.
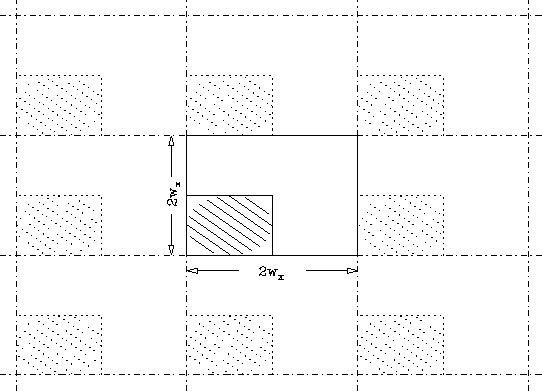
Figure 3: Doubled region for FFT.
The solid frame indicates the doubled region for FFT and its left-bottom
quadrant is the charge region ![]() . The region hatched by
solid lines is the real charge region and that by dotted lines the
ghost charge due to the periodicity of Fourier transformation.
. The region hatched by
solid lines is the real charge region and that by dotted lines the
ghost charge due to the periodicity of Fourier transformation.
The obtained values of the potential are those at cell centers.
They are interpolated by 2-dimensional cubic spline and
differentiated to get ![]() and
and
![]() .
.
When a charged particle gets out of the mesh region, the field created by it is ignored in CAIN. However, the force by the other beam is taken into account even if the particle is outside the mesh region of the other beam. To this end, CAIN adopts three methods, namely, [A] direct Coulomb force by the charge distribution in the mesh, [B] harmonic expansion in polar coordinate, and [C] harmonic expansion in elliptic coordinate.
Let ![]() be the total width of the mesh region.
If it is close to a square, or more precisely, if
be the total width of the mesh region.
If it is close to a square, or more precisely, if ![]() ,
the whole region is divided into three regions [O],[A],[B],
as depicted in Fig.4a. If the mesh region is far from square,
the whole region is divided into four, [O],[A],[B],[C],
as in Fig.4b. In the region [O] the mesh is used for
calculating the field. In other regions, the methods mentioned above are
used.
,
the whole region is divided into three regions [O],[A],[B],
as depicted in Fig.4a. If the mesh region is far from square,
the whole region is divided into four, [O],[A],[B],[C],
as in Fig.4b. In the region [O] the mesh is used for
calculating the field. In other regions, the methods mentioned above are
used.
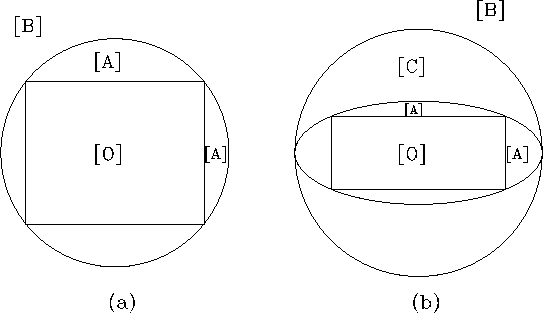
Figure 4: Regions for calculating the beam field
Since the sum is time consuming,
this is used only in region [A], where two other methods fail to converge.
The method is trivial and given by
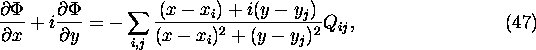
However, this formula is not accurate when the bin size ratio
![]() is far from unity. It is needed to take
average over a bin when the bin is close to the field point (x,y).
CAIN makes a table for the Coulomb force by a bin (
is far from unity. It is needed to take
average over a bin when the bin is close to the field point (x,y).
CAIN makes a table for the Coulomb force by a bin (![]() )
for faster computation.
)
for faster computation.
In the region [B] the following formula is used.
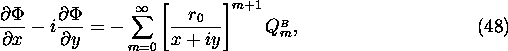
![]()
Here, ![]() is arbitrary (introduced for avoiding overflow/underflow).
The formula is valid for
is arbitrary (introduced for avoiding overflow/underflow).
The formula is valid for ![]() , where
, where ![]() =
= ![]() is the maximum radius
of the mesh region.
is the maximum radius
of the mesh region.
When ![]() (otherwise, exchange x and y), the elliptic coordinate
(u,v) defined by
(otherwise, exchange x and y), the elliptic coordinate
(u,v) defined by
![]()
is used. Here, f is chosen as
![]()
The maximum of the radial-like coordinate u in the mesh region is
![]()
which is taken at the four corners.
Then, the expansion of ![]() is
is
![]()
![]()
Actually, there is a finite relation between ![]() and
and
![]() :
:
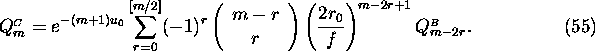
The formula converges if ![]() , which corresponds to the region
[C] (and [B]) in Fig.4b.
The truncation of the series is defined by the operand NMOM
of the command BBFIELD (common to the two types of expansions
for simplicity).
, which corresponds to the region
[C] (and [B]) in Fig.4b.
The truncation of the series is defined by the operand NMOM
of the command BBFIELD (common to the two types of expansions
for simplicity).