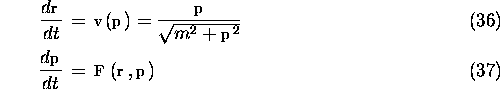
The force
Solving the equation of motion in PUSH command is much more complicated
because of the possible presense of the beam field.
The equation of motion is in general written in the form
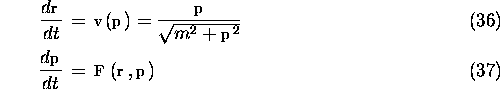
The force ![]() includes the beam field and the external field.
The
includes the beam field and the external field.
The ![]() dependence of
dependence of ![]() comes from
comes from ![]() although very weak in the case of the beam field.
although very weak in the case of the beam field.
Given the initial variables ![]() , a simple
approximation after the time interval
, a simple
approximation after the time interval ![]() is
is
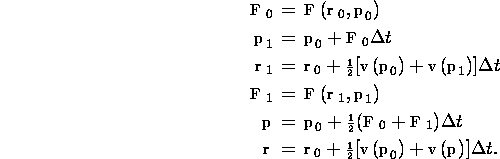
The error of ![]() by these formulas is estimated by
by these formulas is estimated by
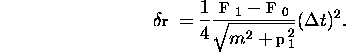
If this is not small enough, divide the interval ![]() by an integer
by an integer ![]() .
Note that
.
Note that ![]() because
because ![]() is proportional to
is proportional to ![]() . The total error, after multiplied by the
number of intervals
. The total error, after multiplied by the
number of intervals ![]() , is proportional to
, is proportional to ![]() .
.
However, the above prescription is not really enough when there are
extremely low energy particles (e.g., those from incoherent pair creation).
It often happens that ![]() so determined bocomes over several hundreds.
In such a case the above error estimation may not be accurate at all.
so determined bocomes over several hundreds.
In such a case the above error estimation may not be accurate at all.
When ![]() is too large, CAIN tries the fourth-order Runge-Kutta integration.
Starting from the whole interval
is too large, CAIN tries the fourth-order Runge-Kutta integration.
Starting from the whole interval ![]() , it is divided by 2 at each step
until the difference becomes small enough. This method is a little better
than the simple formulas above but is still time consuming.
So, the users should be aware that incoherent pair creation is expensive.
, it is divided by 2 at each step
until the difference becomes small enough. This method is a little better
than the simple formulas above but is still time consuming.
So, the users should be aware that incoherent pair creation is expensive.