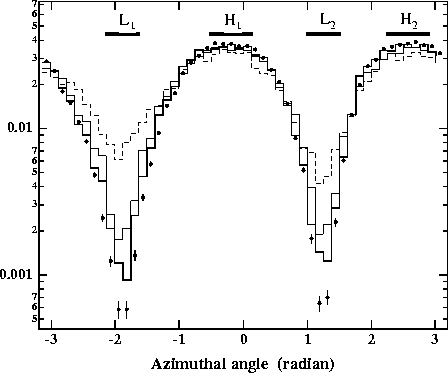
Figure 7:
Azimuthal angular distributions measured for 6< r < 7cm
at z=+1m for R=85.5(solid circles), 42.8(solid line), 28.5(dotted
one) and 8.55(dashed one) corresponding to 
,
2
, 3 and 10,
respectively. The distributions are normalized by the total number of
particles. The angular regions of 
(left), 
(right),
(down) and 
(up) are also shown.
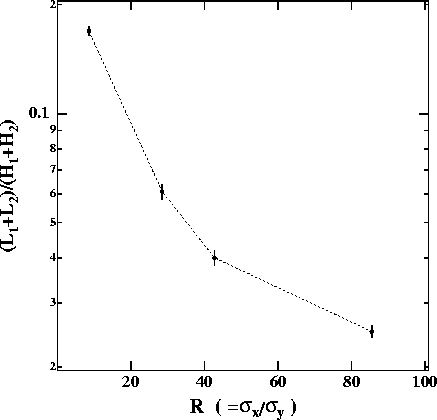
Figure 8:
Number of particles in and normalized by that
in and as a function of R. The same data are used as
in the previous figure. The errors are statistical, corresponding to
160 bunch crossings, except for the lowest R, which corresponds to
800 bunch crossings.
Figure 7 shows the azimuthal angular distributions
measured for 6< r < 7cm at z=+1m for various values of
's, where 4 angular regions are defined for further
numerical studies, i.e. (left)
,
(right)
, (down)
and (up)
. By comparing this
figure with Fig.4 we can clearly see that the
linear dependence on R of the yields in the depletion region is
preserved through the motion in the solenoid. The effect of the
horizontal crossing can still be seen in Fig.7; that is,
there is more depletion on the left side() than on the right
(). The numbers of particles are expected to be 2.4, 3.5, 120,
and 120 per single-bunch crossing in , , and ,
respectively, under the nominal beam condition. The statistics
will actually be much better because the beam pulse contains 72
bunches. Thus, there will be no problem in the statistical
sensitivity for this measurement, although the yields decrease
inversely proportional to . The ratio of 
is plotted as a function of R in Fig.8.
Actually, this ratio depends only on R, as expected by
Eq.13. Since 
is measured from 
,
we can obtain 
by this azimuthal angular
distribution. The statistical accuracy will be less than
0.1 with a few pulse-train crossings if no
significant background exists.