(similarly for y), where N is the beam intensity, 2L the bunch length,
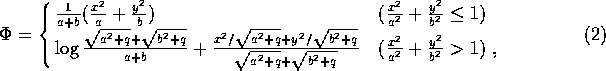
where q(x,y) is the positive solution to the equation
where
The equation of motion of a same-charge particle during a beam-beam collision is expressed by[5]
![]()
(similarly for y), where N is the beam intensity, 2L the bunch
length, ![]() the classical electron radius,
the classical electron radius, ![]() the Lorentz
factor of the beam energy and
the Lorentz
factor of the beam energy and ![]() the energy fraction of the
particle. For a uniform charge distribution inside an elliptic
cylinder of 2L long with radii a and b in the horizontal(x)
and vertical(y) directions, respectively, the Coulomb potential is
exactly given by
the energy fraction of the
particle. For a uniform charge distribution inside an elliptic
cylinder of 2L long with radii a and b in the horizontal(x)
and vertical(y) directions, respectively, the Coulomb potential is
exactly given by
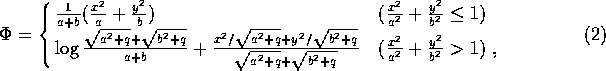
where q(x,y) is the positive solution to the equation ![]() . Assuming that a particle is created
uniformly at a position
. Assuming that a particle is created
uniformly at a position ![]() with zero scattering
angle
with zero scattering
angle ![]() , its trajectory inside the
ellipsoid is
, its trajectory inside the
ellipsoid is
![]()
![]()
where ![]() is the aspect ratio of the transverse beam
profile, which is equivalent to
is the aspect ratio of the transverse beam
profile, which is equivalent to ![]() for a Gaussian
beam.
for a Gaussian
beam.
We first consider the azimuthal angular distribution of
same-charge particles while ignoring the Coulomb field outside of the
cylinder. The azimuthal angle (![]() ) is defined by
) is defined by
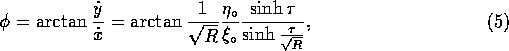
where
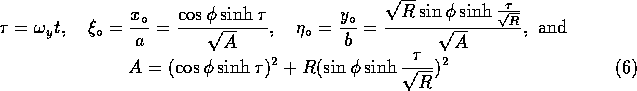
under the condition
![]()
The distribution function (![]() ), which is normalized to unity,
is expressed by
), which is normalized to unity,
is expressed by
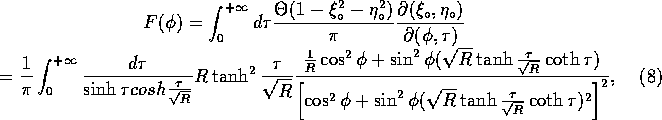
where ![]() is a step function.
For
is a step function.
For ![]() and
and ![]() (or
(or ![]() ), where we are
interested in measuring the aspect ratio for future linear
colliders,
), where we are
interested in measuring the aspect ratio for future linear
colliders, ![]() can be well approximated as
can be well approximated as
![]()
As can be clearly seen in the above
equations(8,9), the
distribution in the angular region near to the horizontal plane is
depleted for a large aspect ratio as 1/R. On the contrary, the
distribution in the vertical direction ![]() has
apparently no dependence on R. Therefore, we hereafter concentrate
on calculations near to the horizontal plane in this section. We then
estimate the effect of the Coulomb force outside of the elliptic
cylinder, where the equation of motion is approximated for
has
apparently no dependence on R. Therefore, we hereafter concentrate
on calculations near to the horizontal plane in this section. We then
estimate the effect of the Coulomb force outside of the elliptic
cylinder, where the equation of motion is approximated for ![]() and
and ![]() , as follows:
, as follows:
![]()
and
![]()
Since the vertical force in Eq.(11) is very small
in this region, except for ![]() , we neglect it for the moment.
Integrating the x component of Eq.(10) once, for
large
, we neglect it for the moment.
Integrating the x component of Eq.(10) once, for
large ![]() we obtain
we obtain
![]()
where ![]() and
and ![]() , which is the x-velocity at the
position (x, y) = (a, 0) . The resultant distribution function at
, which is the x-velocity at the
position (x, y) = (a, 0) . The resultant distribution function at
![]() is give for large
is give for large ![]() by
by
![]()
We further estimated the effect of the vertical force neglected in
the above calculation by numerically integrating
Eqs.(10) and (11). The major
effect was found to be an overall change in the magnitude by a
constant factor of ![]() . Therefore, the R dependence of
F(0) becomes
. Therefore, the R dependence of
F(0) becomes ![]() instead of 1 / R (
Eq.(9)) mainly due to a horizontal force
outside of the elliptic cylinder. Thus, for the case of a flat beam (
instead of 1 / R (
Eq.(9)) mainly due to a horizontal force
outside of the elliptic cylinder. Thus, for the case of a flat beam (![]() ), the same-charge particles are strongly
deflected in the vertical direction; their azimuthal angular
distribution gives us direct information about R. It should also be
noticed that the particles tend to be deflected more in a direction
where their creation points are displaced by
), the same-charge particles are strongly
deflected in the vertical direction; their azimuthal angular
distribution gives us direct information about R. It should also be
noticed that the particles tend to be deflected more in a direction
where their creation points are displaced by ![]() and
and
![]() , since the forces are proportional to
, since the forces are proportional to ![]() and
and ![]() , respectively, provided by
differentiating Eq.(2). This gives us the sensitivity
to measure the alignment between two beams, which is discussed in the
next section.
, respectively, provided by
differentiating Eq.(2). This gives us the sensitivity
to measure the alignment between two beams, which is discussed in the
next section.
The maximum deflection angle for low-energy particles can be
expressed by[5]
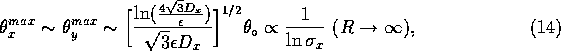
where ![]() ,
, ![]() ,
, ![]() and
and ![]() . Using these
relations, Gaussian beams
. Using these
relations, Gaussian beams ![]() can be
well described in terms of variables (a,b,L) of an elliptic
cylinder. Assuming that the beam intensity and the bunch length are
known, the horizontal beam size can be obtained from a measurement
of the maximum deflection angle, especially for a large aspect ratio,
as can be clearly seen in Eq.(14).
can be
well described in terms of variables (a,b,L) of an elliptic
cylinder. Assuming that the beam intensity and the bunch length are
known, the horizontal beam size can be obtained from a measurement
of the maximum deflection angle, especially for a large aspect ratio,
as can be clearly seen in Eq.(14).