To treat the Bethe-Heitler , Landau-Lifshitz and the Bremsstrahlung processes, the so-called almost-real-photon approximation, or equivalent photon approximation, or Weizacker-Williams approximation, is employed. An electron is accompanied by virtual photons which look like real photons at ultra-relativistic limit. They interact with on-coming (real or virtual) photons incoherently. Thus, the Bethe-Heitler and Landau-Lifshitz processes above are reduced to the Breit-Wheeler process and the Bremsstrahlung to the Compton process:
Let the electron energy be ![]() (
(![]() ). The number of
virtual photons with energy
). The number of
virtual photons with energy ![]() and transverse momentum
and transverse momentum
![]() is given by
is given by
![]()
where ![]() is the fine structure constant. For given
is the fine structure constant. For given ![]() ,
the typical transverse momentum is very small,
,
the typical transverse momentum is very small, ![]() ,
so that it is not important in collision kinematics but, instead, the
finite transverse extent
,
so that it is not important in collision kinematics but, instead, the
finite transverse extent ![]() can bring about significant
effects. In the (transverse) configuration space, the above expression
becomes
can bring about significant
effects. In the (transverse) configuration space, the above expression
becomes
![]()
where ![]() is the transverse coordinate with respect to the
parent electron,
is the transverse coordinate with respect to the
parent electron, ![]() , and
, and ![]() the modified
Bessel function.
the modified
Bessel function.
The transverse momentum cut off ![]() (or
(or ![]() ) is somewhat umbiguous. It should depend on the
momentum transfer of the whole process. This dependence is ignored in CAIN
because the virtual photons are generated independently from the
following processes and because it does not much affect the low energy pairs.
) is somewhat umbiguous. It should depend on the
momentum transfer of the whole process. This dependence is ignored in CAIN
because the virtual photons are generated independently from the
following processes and because it does not much affect the low energy pairs.
The lower limit ![]() of the integration over
of the integration over ![]() is, in our case,
determined by the pair creation threshold.
Let us introduce dimensionless variables
is, in our case,
determined by the pair creation threshold.
Let us introduce dimensionless variables ![]() ,
,
![]() , and
, and ![]() . The total number of
the virtual photons is given by
. The total number of
the virtual photons is given by![]()
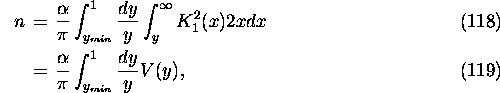
with
![]()
When ![]() , the total number is
, the total number is
![]()
where ![]() is Euler's constant.
At very high energies the number of virtual photons per electron
is O(1), in spite of the small factor
is Euler's constant.
At very high energies the number of virtual photons per electron
is O(1), in spite of the small factor ![]() ,
due to the factor
,
due to the factor ![]() .
.
1ex
When Bethe-Heitler and/or Landau-Lifshitz processes are specified by PPINT command, CAIN generates virtual photons in each longitudinal slice at each time step and counts them in the same mesh as that generated by the LUMINOSITY command. The number of macro-virtual photons is somewhat arbitrary. In the present version it is determined such that the weight of the macro-virtual photons is equal to the maximum weight of the electrons in the on-coming beam (not equal to the weight of each parent electron in order to prevent low-weight electrons from generating many photons).
Since the y (energy) spectrum is approximately proportional to
![]() for small y, the spectrum becomes almost flat if one chooses
for small y, the spectrum becomes almost flat if one chooses ![]() as the primary variable. To account for relatively large y too, CAIN
adopts the variable
as the primary variable. To account for relatively large y too, CAIN
adopts the variable ![]() instead of y:
instead of y:
![]()
Here, c>0 is introduced so that the function ![]() defined later, is finite.
It is chosen to be 0.2 but is almost arbitrary provided
defined later, is finite.
It is chosen to be 0.2 but is almost arbitrary provided ![]() .
The maximum
.
The maximum ![]() is
is
![]()
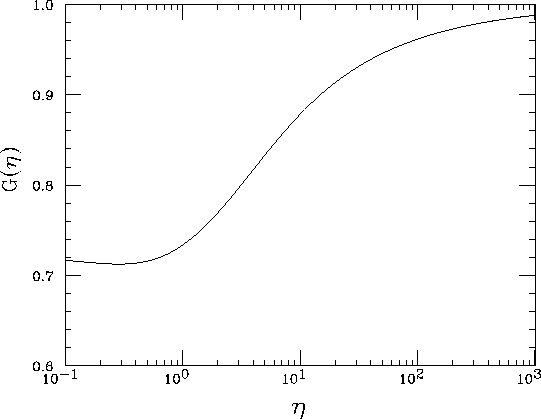
Figure 11: Function ![]() defined in eq.(125). It is close to
unity because only large
defined in eq.(125). It is close to
unity because only large ![]() region is important. G(0) is finite and
depends on the
parameter c. G(0)<1 if
region is important. G(0) is finite and
depends on the
parameter c. G(0)<1 if ![]() . Here, c=0.2
is adopted.
. Here, c=0.2
is adopted.
Now, the spectrum with respect to ![]() is
is
![]()
with
![]()
For ![]() ,
, ![]() and close to 1 except for the small
and close to 1 except for the small ![]() region which is umimportant in practice. Thus,
region which is umimportant in practice. Thus,
![]()
For given ![]() (or y) the distribution of x is proportional to
dV(x)/V(y) and, therefore, can be random-generated by using inverse function
(or y) the distribution of x is proportional to
dV(x)/V(y) and, therefore, can be random-generated by using inverse function
![]() .
.
The algorithm is as follows.