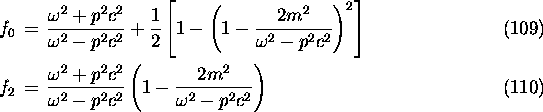Next: Virtual (almost real) photon
Up: Incoherent Pair Production
Previous: Incoherent Pair Production
The differential crosssection with respect to the scattering angle
of the final electron in the center-of-mass frame is given by
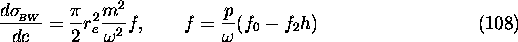
with
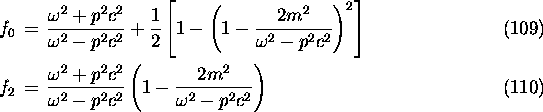
where
 , p
, p
- Energy and momentum of final electron
in the center-of-mass frame.
- c
- Cosine of the scattering angle
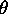 of the final electron in the center-of-mass frame.
of the final electron in the center-of-mass frame.
- h
- Product of circular polarizations of the two initial photons.
The total crosssection is

where
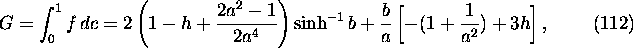
where
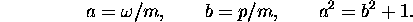
Events are generated by the following algorithm using inverse function.
- (a)
- Compute
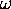 , p, a, b, G and
, p, a, b, G and 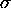 for given
initial parameters (reject if
for given
initial parameters (reject if 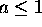 , i.e., below threshold)
and calculate the event probability for the given time step
, i.e., below threshold)
and calculate the event probability for the given time step
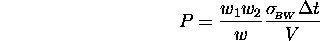
where 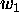 and
and 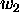 are the weights of initial photons
(number of real photons divided by that of macro photons), w the
weight of the pair to be created,
are the weights of initial photons
(number of real photons divided by that of macro photons), w the
weight of the pair to be created, 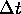 the time interval
and V the volume in which the macro phtons are located.
the time interval
and V the volume in which the macro phtons are located.
- (b)
- If P is too large (say, >0.1), divide the interval
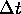 (and P) by an integer
(and P) by an integer 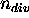 ,
and repeat the following procedure
,
and repeat the following procedure 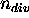 times.
times.
- (c)
- Generate a random number
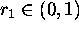 .
Reject if
.
Reject if 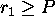 .
.
- (d)
- Generate another random number
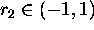 and solve the equation
and solve the equation
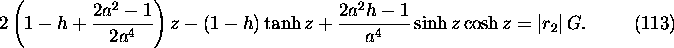
with respect to z.
Here z is defined by 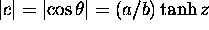 (
(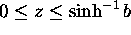 ). The left hand side is the integral
of f from 0 to
). The left hand side is the integral
of f from 0 to 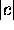 . The sign of
. The sign of 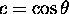 is determined by the sign of
is determined by the sign of 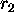 .
.
- (e)
- Generate another random number
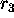
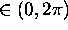 and
compute the transverse component of electron momentum by
and
compute the transverse component of electron momentum by
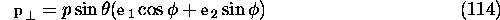
where 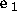 and
and 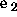 are arbitrary unit vectors
perpendicular to
are arbitrary unit vectors
perpendicular to 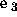 , the unit vector along the initial photon
momentum in the center-of-mass frame. The latter is given by
, the unit vector along the initial photon
momentum in the center-of-mass frame. The latter is given by
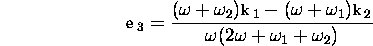
where 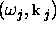 are the energy momentum of the
photons in the original frame.
are the energy momentum of the
photons in the original frame.
The value of 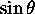 should be computed from
should be computed from
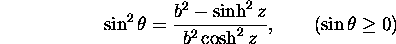
rather than from 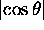 because the latter is usually very
close to unity when
because the latter is usually very
close to unity when 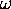 is much larger than
the electron rest mass.
is much larger than
the electron rest mass.
- (f)
- Then, the momentum of the electron in the original frame
is calculated by
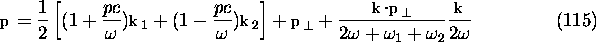
where 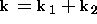 .
Note that
.
Note that 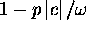 must be computed from
must be computed from
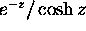 in order to avoid round off errors.
in order to avoid round off errors.
- (g)
- The momentum of positron is computed from the momentum
conservation.





Next: Virtual (almost real) photon
Up: Incoherent Pair Production
Previous: Incoherent Pair Production
Toshiaki Tauchi
Thu Dec 3 17:27:26 JST 1998
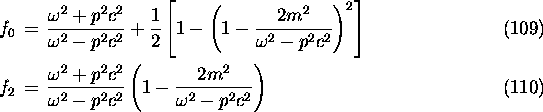
![]()