Theoretically, the luminosity spectrum is determined by a set of beam parameters:
the horizontal, vertical and longitudinal beam sizes (![]() ) and the
number of particles in a bunch(N). In the empirical function, two independent-valuables
appeared as
) and the
number of particles in a bunch(N). In the empirical function, two independent-valuables
appeared as ![]() and
and ![]() . They can be calculated from the
measured spectrum, since the measured one is the luminosity spectrum convoluted by the cross
section of the Bhabha scattering process, which is called the weighted luminosity spectrum.
In this analysis, one of them is obtained by assuming a fixed value of the other, and vice
versa, i.e. one parameter fitting in a likelihood method. The beam energy was set
to be 250 GeV and the relevant parameters are listed in Table 14.1, which are called
``nominal" beam parameters.
. They can be calculated from the
measured spectrum, since the measured one is the luminosity spectrum convoluted by the cross
section of the Bhabha scattering process, which is called the weighted luminosity spectrum.
In this analysis, one of them is obtained by assuming a fixed value of the other, and vice
versa, i.e. one parameter fitting in a likelihood method. The beam energy was set
to be 250 GeV and the relevant parameters are listed in Table 14.1, which are called
``nominal" beam parameters.
For this study, two kinds of Bhabha events were generated by the method described in the
previous section. They are called an `experimental-data sample' (e-sample) and a
`likelihood-function sample' (l-sample). The Monte Carlo statistics of e-samples corresponds
to 10fb![]() and 1fb
and 1fb![]() for the angular regions of
for the angular regions of ![]() and
and ![]() , respectively. The polar angles of electrons and positrons in the Bhabha events
were smeared with a Gaussian distribution of 1mrad resolution; then, the weighted
luminosity-spectrum was calculated as a function of
, respectively. The polar angles of electrons and positrons in the Bhabha events
were smeared with a Gaussian distribution of 1mrad resolution; then, the weighted
luminosity-spectrum was calculated as a function of ![]() from their acollinearity
angles. A number of e-samples were generated with several sets of B and
from their acollinearity
angles. A number of e-samples were generated with several sets of B and ![]() . To
determine a likelihood function, a l-sample was generated with 10 times more statistics than
the e-samples with the nominal beam parameters. The weighted luminosity spectrum was
obtained in the same way as the e-sample. Dividing the spectrum into 50 bins for 450
. To
determine a likelihood function, a l-sample was generated with 10 times more statistics than
the e-samples with the nominal beam parameters. The weighted luminosity spectrum was
obtained in the same way as the e-sample. Dividing the spectrum into 50 bins for 450![]() 500GeV, the normalized likelihood function
500GeV, the normalized likelihood function ![]() was defined by
was defined by
![]()
where ![]() is the bin-number corresponding to
is the bin-number corresponding to ![]() ,
,
![]() is the number of events in the
is the number of events in the ![]() 'th bin, and
'th bin, and
![]() is the total event number of the l-sample.
For the e-sample, the log-likelihood was calculated by
is the total event number of the l-sample.
For the e-sample, the log-likelihood was calculated by
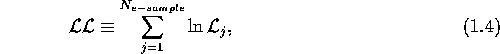
where ![]() is the total event number of the e-sample and
is the total event number of the e-sample and
![]() is the likelihood of the j'th
event in the e-sample.
is the likelihood of the j'th
event in the e-sample.
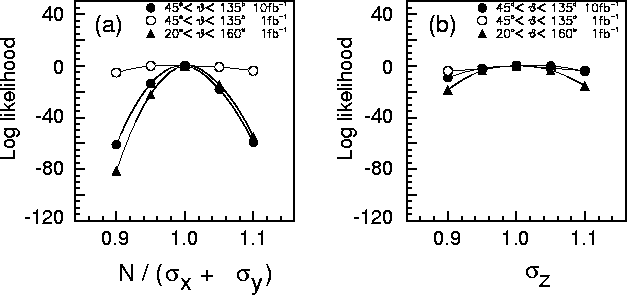
Figure 14.23:
Log-likelihood distributions of the e-samples as a function of (a)
![]() and (b)
and (b) ![]() , where the parameter was
varied for
, where the parameter was
varied for ![]() 10% relative to the nominal value, while the other was fixed to the
nominal value and vice versa.
10% relative to the nominal value, while the other was fixed to the
nominal value and vice versa.
Figures 14.23(a) and (b) show the log-likelihood distributions as a function of B
and ![]() , respectively. From these figures, it can be seen that the beam parameter of
B or
, respectively. From these figures, it can be seen that the beam parameter of
B or
![]() can be determined with an accuracy of several % by large (
can be determined with an accuracy of several % by large (![]() ) and
small(
) and
small(![]() ) angle Bhabha events for an integrated luminosity of
10fb
) angle Bhabha events for an integrated luminosity of
10fb![]() and 1fb
and 1fb![]() , respectively.
, respectively.
As described in the previous section, since the energy scan should be made for the integrated
luminosity of a few fb![]() each at a number of CM energies around toponium resonance
states[2], a 1 mrad angular resolution must be necessary in the small angular region
(
each at a number of CM energies around toponium resonance
states[2], a 1 mrad angular resolution must be necessary in the small angular region
(![]() ). In these cases, the integrated luminosity of the peak in the
luminosity spectrum must be precisely determined, although the peak may be smeared by the
beam energy spread. It is seen that the present study has demonstrated the feasibility toward
this end.
). In these cases, the integrated luminosity of the peak in the
luminosity spectrum must be precisely determined, although the peak may be smeared by the
beam energy spread. It is seen that the present study has demonstrated the feasibility toward
this end.