where
For Bhabha events, the momentum difference (![]() ) between
) between ![]() - and
- and ![]() -beams
can be expressed by
-beams
can be expressed by
![]()
where ![]() is the acollinearity angle,
is the acollinearity angle, ![]() is the
nominal beam momentum, and
is the
nominal beam momentum, and ![]() is the average of
is the average of ![]() and
and ![]() polar angles.
polar angles.
Thus, the momentum difference can be calculated from the acollinearity angles of
Bhabha events for the known nominal beam energy.
The center-of-mass(CM) energy (![]() ) can be calculated using
) can be calculated using
![]()
where ![]() is the nominal CM energy, i.e.
is the nominal CM energy, i.e. ![]() for
head-on collisions. Since
for
head-on collisions. Since ![]() is larger than zero,
is larger than zero, ![]() must be less
than (or equal to)
must be less
than (or equal to)
![]() . The beam-energy spread also produces events over the nominal
beam-energy, as shown in Figure 14.19(a), while the
. The beam-energy spread also produces events over the nominal
beam-energy, as shown in Figure 14.19(a), while the ![]() distribution is
always below the nominal one as shown in Fig14.19(b). This is a limitation of this
technique. In order to overcome this limitation for a sizable spread, we need
additional information, such as the energies of scattered electrons and positrons.
distribution is
always below the nominal one as shown in Fig14.19(b). This is a limitation of this
technique. In order to overcome this limitation for a sizable spread, we need
additional information, such as the energies of scattered electrons and positrons.
Now, to separately examine the effects of the finite angular resolution of the detector, the
beam energy spread is turned off. The measured spectrum with a perfect detector, i.e.
with a perfect angular resolution, is compared with those with angular
resolutions (![]() ) of 3 mrad and 5 mrad in Figure 14.20. In a simulation
the polar angles of both tracks are smeared by Gaussian distributions with the assumed angular
resolution.
) of 3 mrad and 5 mrad in Figure 14.20. In a simulation
the polar angles of both tracks are smeared by Gaussian distributions with the assumed angular
resolution.
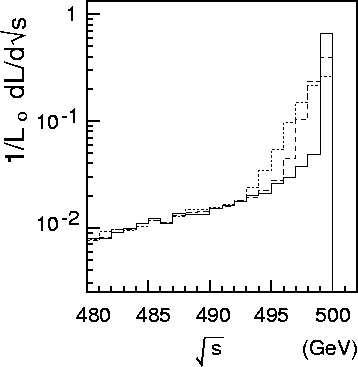
Figure 14.20:
Luminosity-spectra as measured by the acollinearity angles of the Bhabha events.
Various angular resolutions of measuring the Bhabha scattered particles are
considered. Solid, dashed and dotted histograms correspond to angular resolutions of
![]() =0(perfect), 3mrad and 5mrad, respectively.
=0(perfect), 3mrad and 5mrad, respectively.
The statistics of the simulation in Figure 14.19 corresponds to an accumulated
luminosity of 10fb![]() (about one year accumulation). The detector is assumed to cover the
polar angular region from 45
(about one year accumulation). The detector is assumed to cover the
polar angular region from 45![]() to 135
to 135![]() . Since the observed spectrum with
. Since the observed spectrum with
![]() mrad resolution is hardly distinguishable from the perfect detector case,
it is not independently plotted in Figure 14.20. The spectrum with
mrad resolution is hardly distinguishable from the perfect detector case,
it is not independently plotted in Figure 14.20. The spectrum with ![]() 3 mrad shows a significant smearing effect.
3 mrad shows a significant smearing effect.
For studies of toponium physics, accurate knowledge of the luminosity-spectrum within the
total decay width of the top quark is very important. The top quark decay width is estimated
to be 1.55GeV for ![]() 175 GeV, i.e.
175 GeV, i.e. ![]() 0.5% of
0.5% of ![]() , according
to the standard model. The performance of the accolinearity angle method in this narrow energy
region needs to be examined. For this purpose, the integral luminosity for 455
, according
to the standard model. The performance of the accolinearity angle method in this narrow energy
region needs to be examined. For this purpose, the integral luminosity for 455![]() 450GeV to actually be obtained in collisions, and the luminosity values to be ``measured" by
this method are compared. Figure 14.21 shows the results of this study. The
``nominal" (i.e. actual) luminosity is compared with the ``measured" luminosity where
various detector angular resolutions and polar angle coverages are assumed. It can be seen
that an angular resolution better than 3 mrad is required for
450GeV to actually be obtained in collisions, and the luminosity values to be ``measured" by
this method are compared. Figure 14.21 shows the results of this study. The
``nominal" (i.e. actual) luminosity is compared with the ``measured" luminosity where
various detector angular resolutions and polar angle coverages are assumed. It can be seen
that an angular resolution better than 3 mrad is required for ![]() to maintain
a satisfactory luminosity measurement performance. We also observed a slightly higher
luminosity by 2.5% than the nominal one, even with the perfect resolution in
Figure 14.21, since a small amount of luminosity must be added in a case that both
beams can loose the same energies with no acollinearity angle, where
to maintain
a satisfactory luminosity measurement performance. We also observed a slightly higher
luminosity by 2.5% than the nominal one, even with the perfect resolution in
Figure 14.21, since a small amount of luminosity must be added in a case that both
beams can loose the same energies with no acollinearity angle, where
![]() , by Equations 14.1 and
14.2.
, by Equations 14.1 and
14.2.
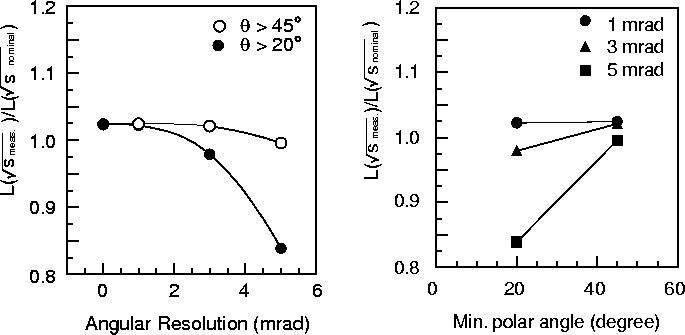
Figure 14.22:
Luminosity normalized by the nominal one at ![]() GeV as a function of
the minimum polar angle to be measured for various angular resolutions.
GeV as a function of
the minimum polar angle to be measured for various angular resolutions.
Figure 14.21:
Luminosity normalized by the nominal one at ![]() GeV as a function of
GeV as a function of
![]() in two angular regions of
in two angular regions of ![]() (open circles) and
(open circles) and ![]() (solid circles).
(solid circles).
When Bhabha-scattered particles within a smaller polar angle region are included in the
analysis the angular resolution of the measurement needs to be substantially improved
because of a factor ![]() in Equation 14.1.
On the other hand, the statistics of the Bhabha events increases very rapidly with decreasing
the minimum polar angle (
in Equation 14.1.
On the other hand, the statistics of the Bhabha events increases very rapidly with decreasing
the minimum polar angle (![]() ) to be measured. For example, the statistics for
) to be measured. For example, the statistics for
![]() =20
=20![]() increases by about one order of magnitude compared to that of
increases by about one order of magnitude compared to that of
![]() =45
=45![]() ; therefore, the integrated luminosity can be reduced to 1fb
; therefore, the integrated luminosity can be reduced to 1fb![]() in the requirement. As shown in Figures 14.21 and 14.22, the angular
resolution must be at least 1 mrad for
in the requirement. As shown in Figures 14.21 and 14.22, the angular
resolution must be at least 1 mrad for
![]() =20
=20![]() . The toponium experiment will involve an energy scan. It
will consist of operations at several energy points each for a few
fb
. The toponium experiment will involve an energy scan. It
will consist of operations at several energy points each for a few
fb![]() [2]. Therefore, it is essential to have
[2]. Therefore, it is essential to have ![]() 1 mrad
for
1 mrad
for ![]() 20
20![]() . The higher statistics is also favored in the light of reducing
any possible systematic errors in the measurement of the luminosity.
. The higher statistics is also favored in the light of reducing
any possible systematic errors in the measurement of the luminosity.