

Next: Impact Parameter Resolution
Up: Examples of Applications
Previous: Examples of Applications
In the case of no multiple scattering,
the momentum resolution for a tracking detector with
(n+1) equally spaced sampling points is given by
Eq.B.9 through
| 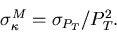 |
(104) |
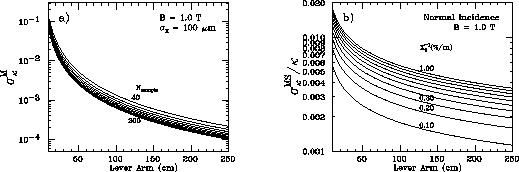
We plotted 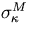 in Fig.3.1-a)
as a function of lever arm length for different numbers of
sampling points.
Notice that we set
in Fig.3.1-a)
as a function of lever arm length for different numbers of
sampling points.
Notice that we set 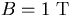 and
and 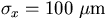 there to ease the
conversion to different B or
there to ease the
conversion to different B or 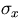 values:
values: 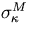 is
inversely proportional to B, while it is proportional to
is
inversely proportional to B, while it is proportional to 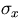 .
.
The multiple scattering in the tracking volume
adds 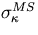 given by Eq.3.2.56
to the above measurement error in quardrature
(see Eq.3.2.48).
Fig.3.1-b) shows
given by Eq.3.2.56
to the above measurement error in quardrature
(see Eq.3.2.48).
Fig.3.1-b) shows 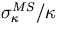 as
a function of the lever arm length for different values of
material thickness in the tracking device.
as
a function of the lever arm length for different values of
material thickness in the tracking device.
Figure 3.1:
(a) The reciprocal transverse momentum resolution as a function of
lever arm length for 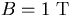 ,
, 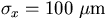 , and
, and 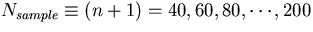 . (b) The multiple scattering contribution as a function of lever arm
length for
. (b) The multiple scattering contribution as a function of lever arm
length for 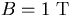 and
and 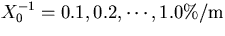 .
.
 |
Keisuke Fujii
12/4/1998
![]() given by Eq.3.2.56
to the above measurement error in quardrature
(see Eq.3.2.48).
Fig.3.1-b) shows
given by Eq.3.2.56
to the above measurement error in quardrature
(see Eq.3.2.48).
Fig.3.1-b) shows ![]() as
a function of the lever arm length for different values of
material thickness in the tracking device.
as
a function of the lever arm length for different values of
material thickness in the tracking device.
