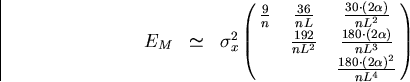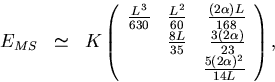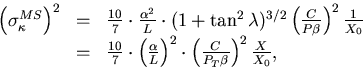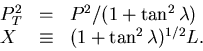

Next: Track Fitting in r-z
Up: Track Fitting in r-
Previous: Inclusion of Multiple Scattering
When the track is affected by multiple scattering during its
coordinate measurements the error matrix (E0 in Eq.3.2.15)
should take that into account.
To see how to implement multiple scattering, let us start with the
modification of the track equation (Eq.3.2.7):
where we have set (x0,y0) = (0,0) and 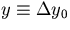 .Multiple scattering modifies
.Multiple scattering modifies 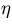 by
by
| 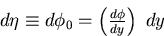 |
(58) |
which necessitates the modification of the track equation![[*]](foot_motif.gif) to
to
| 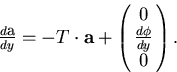 |
(59) |
This means
| 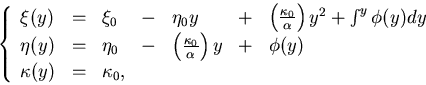 |
(60) |
where the suffix attached to the track track parameters
remines us that they are the track parameters at the
starting point before any multiple scattering.
In the pivot convention taken here (x0,y0) = (0,0),
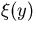 is the x-location of the track.
Therefore, the probability of observing (n+1) hit points,
is the x-location of the track.
Therefore, the probability of observing (n+1) hit points,
 and
and 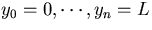 , is
, is
| ![\begin{displaymath}
\begin{array}
{lll}
P_M({\bf x};\phi;{\bf a}_0)
= N ~ \exp...
...;\phi;{\bf a}_0)}
{\sigma_{x_i} }\right)^2 \right],\end{array}\end{displaymath}](img160.gif) |
(61) |
where N is a normalization factor and
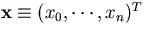 .We must, however, take into account the probability of obtaining
the multiple scattering
.We must, however, take into account the probability of obtaining
the multiple scattering 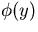 :
:
| ![\begin{displaymath}
\begin{array}
{lll}
P_{MS}(\phi;{\bf a}_0)
& = & N' \exp ...
...c{1}{K}
\left(\frac{d\phi}{dy}\right)^2 dy \right],\end{array}\end{displaymath}](img162.gif) |
(62) |
where use has been made of Eq.3.2.11.
Since we do not know 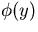 , we should integrate the probability
over
, we should integrate the probability
over 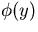 :
:
| ![\begin{displaymath}
\begin{array}
{lll}
\overline{P}({\bf x};{\bf a}_0)
& = &...
...;\phi;{\bf a}_0)}
{\sigma_{x_i} }\right)^2 \right],\end{array}\end{displaymath}](img163.gif) |
(63) |
which now gives the probability of observing
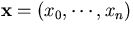 when the track has the
track parameter
when the track has the
track parameter 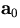 at y=0.
at y=0.
Now, we fit the (n+1) hits to our track model
(Eq.3.1.1) by minimizing
| 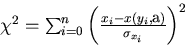 |
(64) |
where 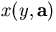 is given by Eq.3.1.1 with x0=0.
Since this problem is linear, we can easily obtain
is given by Eq.3.1.1 with x0=0.
Since this problem is linear, we can easily obtain
| 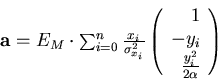 |
(65) |
with
| 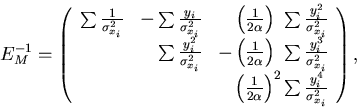 |
(66) |
where EM-1 is the inverse of the error matrix
due to corrdinate measurement errors, for which only
the upper triangle is explicitly shown![[*]](foot_motif.gif) .
Of course, the true error matrix is subsect to the correction for
multiple scattering.
Let us now derive the true error matrix below.
We first note that the displacement of
.
Of course, the true error matrix is subsect to the correction for
multiple scattering.
Let us now derive the true error matrix below.
We first note that the displacement of 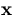 induces the
displacement of
induces the
displacement of 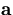 through Eq.3.2.34:
through Eq.3.2.34:
| 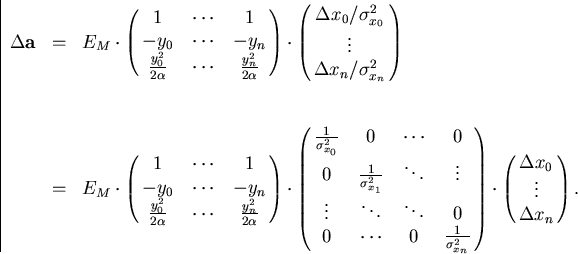 |
(67) |
Defining A and 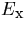 by
by
| 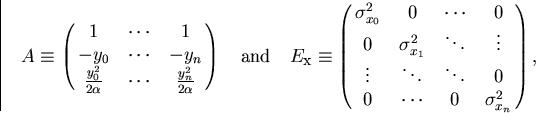 |
(68) |
we can rewrite Eq.3.2.36 as
| 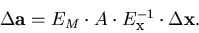 |
(69) |
This equation implies the full error matrix including
multiple scattering to be given by
| 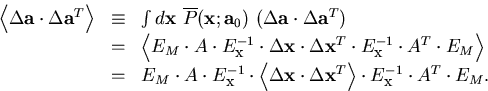 |
(70) |
Notice that in the absence of multiple scattering, we have
and, therefore,
as it should be, where in the last line, we have used
| 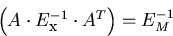 |
(71) |
which can be readily verified.
Our problem is now reduces to how to evaluate
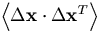 when
the multiple scattering correlates, for instance,
when
the multiple scattering correlates, for instance,
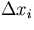 to
to 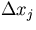 .In order to calculate the correlation matrix, we first note that
.In order to calculate the correlation matrix, we first note that
| 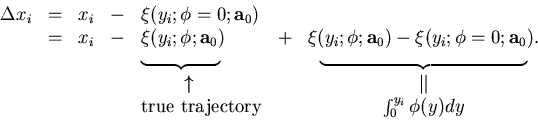 |
(72) |
Substituting this in Eq.3.2.32, we obtain
the following formula for the probability
of getting the measured points 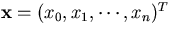 for a track whose track parameter vector at y=y0 is
for a track whose track parameter vector at y=y0 is 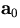 :
:
| ![\begin{displaymath}
\begin{array}
{lll}
\overline{P}({\bf x};{\bf a}_0) & = &
...
...y_i} \phi(y) dy}
{\sigma_{x_i}} \right)^2
\right],\end{array}\end{displaymath}](img183.gif) |
(73) |
which leads us to
The 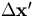 integral is readily performed to yield
integral is readily performed to yield
| 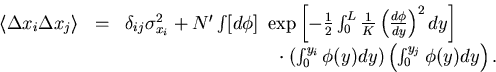 |
(74) |
The second term, which was induced by multiple scattering, has a
familiar path integral form in field theories.
After some straightforward manipulations such as to
divide the path into small segments and to replace integrals by
summentions and differentiations by differences, we arrive at
| 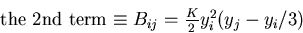 |
(75) |
for 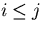 which is enough since B is apparently symmetric.
Combining Eqs.3.2.39, 3.2.46, and 3.2.47,
we obtain the full error matrix as the sum of the part due to
coordinate measurement errors EM
and the part due to
the multiple scattering in the tracking volume EMS:
which is enough since B is apparently symmetric.
Combining Eqs.3.2.39, 3.2.46, and 3.2.47,
we obtain the full error matrix as the sum of the part due to
coordinate measurement errors EM
and the part due to
the multiple scattering in the tracking volume EMS:
| 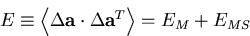 |
(76) |
with
| 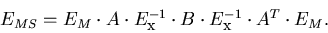 |
(77) |
The calculation of EMS is tedious but doable.
We will, however, restrict ourselves to the case where
the (n+1) samples are equally spaced in y and measured with
an equal accuracy 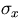 .We fill further assume that n is large,
since the final expression otherwise becomes
too complicated to show here
.We fill further assume that n is large,
since the final expression otherwise becomes
too complicated to show here![[*]](foot_motif.gif) .
The large n limit then gives
.
The large n limit then gives
| 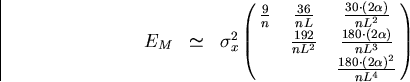 |
(78) |
and
| 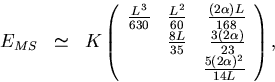 |
(79) |
which, for instance, result in
The error on 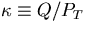 due to multiple scattering is
thus obtained to be
where use has been made of Eq.3.2.11 and
The X is the material thickness through which the track passes.
To see the dependence on the magnetic field explicitly,
we introduce a new constant
due to multiple scattering is
thus obtained to be
where use has been made of Eq.3.2.11 and
The X is the material thickness through which the track passes.
To see the dependence on the magnetic field explicitly,
we introduce a new constant 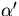 defined by
When we assume
defined by
When we assume 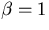 and |Q|=1 (unit charge),
we finally get a familiar result:
and |Q|=1 (unit charge),
we finally get a familiar result:
| 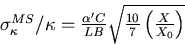 |
(80) |
with
|  |
(81) |


Next: Track Fitting in r-z
Up: Track Fitting in r-
Previous: Inclusion of Multiple Scattering
Keisuke Fujii
12/4/1998
![[*]](foot_motif.gif) to
to
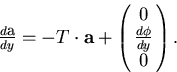
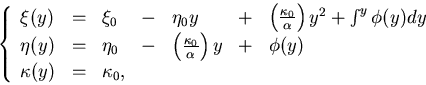
![\begin{displaymath}
\begin{array}
{lll}
P_M({\bf x};\phi;{\bf a}_0)
= N ~ \exp...
...;\phi;{\bf a}_0)}
{\sigma_{x_i} }\right)^2 \right],\end{array}\end{displaymath}](img160.gif)
![\begin{displaymath}
\begin{array}
{lll}
P_{MS}(\phi;{\bf a}_0)
& = & N' \exp ...
...c{1}{K}
\left(\frac{d\phi}{dy}\right)^2 dy \right],\end{array}\end{displaymath}](img162.gif)
![\begin{displaymath}
\begin{array}
{lll}
\overline{P}({\bf x};{\bf a}_0)
& = &...
...;\phi;{\bf a}_0)}
{\sigma_{x_i} }\right)^2 \right],\end{array}\end{displaymath}](img163.gif)
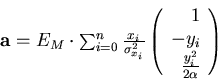
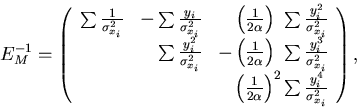
![[*]](foot_motif.gif) .
Of course, the true error matrix is subsect to the correction for
multiple scattering.
Let us now derive the true error matrix below.
We first note that the displacement of
.
Of course, the true error matrix is subsect to the correction for
multiple scattering.
Let us now derive the true error matrix below.
We first note that the displacement of 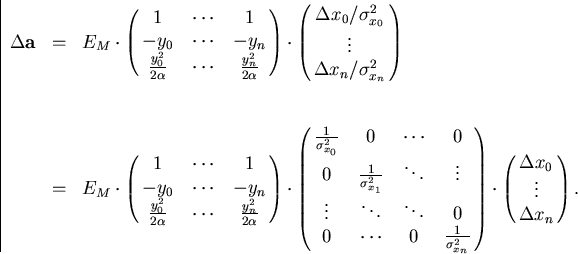
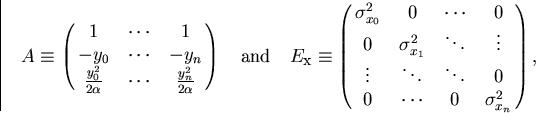
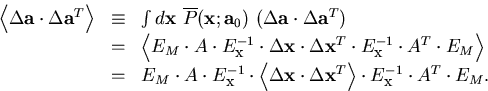
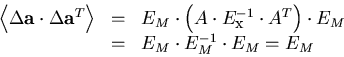
![]() when
the multiple scattering correlates, for instance,
when
the multiple scattering correlates, for instance,
![]() to
to ![]() .In order to calculate the correlation matrix, we first note that
.In order to calculate the correlation matrix, we first note that
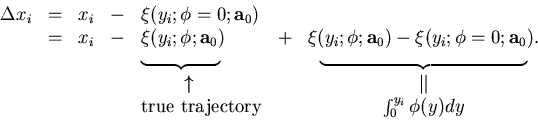
![\begin{displaymath}
\begin{array}
{lll}
\overline{P}({\bf x};{\bf a}_0) & = &
...
...y_i} \phi(y) dy}
{\sigma_{x_i}} \right)^2
\right],\end{array}\end{displaymath}](img183.gif)
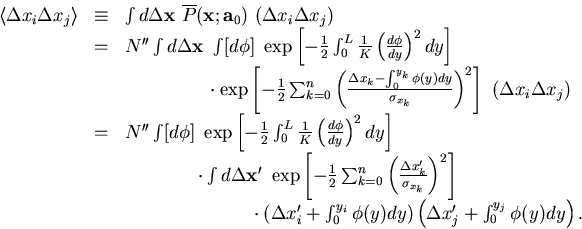
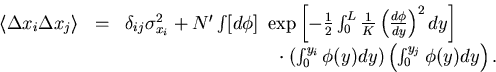
![[*]](foot_motif.gif) .
The large n limit then gives
.
The large n limit then gives