The functions ![]() (k=1,2) are stored in a 5-dimensional array
FF(k,n,i,j,l) (n=1,MPH), (i=0,MY),
(j=0,MXI), (l=0,MLM). The integral over y
from 0 to
(k=1,2) are stored in a 5-dimensional array
FF(k,n,i,j,l) (n=1,MPH), (i=0,MY),
(j=0,MXI), (l=0,MLM). The integral over y
from 0 to ![]() is stored in FINT(k,n,i,j,l).
The integral over the full range
is stored in FINT(k,n,i,j,l).
The integral over the full range ![]() is then
FINT(k,n,MY,j,l)
For integration, the trapezondal rule is used,
which means the function
is then
FINT(k,n,MY,j,l)
For integration, the trapezondal rule is used,
which means the function ![]() is approximated by a piecewise linear function.
The sum of FINT(k,n,MY,j,l) over n is stored in
FALL(k,j,l).
is approximated by a piecewise linear function.
The sum of FINT(k,n,MY,j,l) over n is stored in
FALL(k,j,l).
For a given initial condition, calculate the parameters ![]() and
and ![]() and find FALL(*) by 2-dimensional interpolation.
(The asterisk * indicates the appropriate sum over the
initial polarization, i,e.,
FALL(*)=FALL
and find FALL(*) by 2-dimensional interpolation.
(The asterisk * indicates the appropriate sum over the
initial polarization, i,e.,
FALL(*)=FALL![]() FALL
FALL![]() ).
Then, calculate the total probability P (eq.(131) times the time interval DT):
).
Then, calculate the total probability P (eq.(131) times the time interval DT):
![]()
Generate a uniform random number ![]() in the interval (0,1).
If
in the interval (0,1).
If ![]() , decide to emit a photon and, otherwise reject.
, decide to emit a photon and, otherwise reject.
If rejected, the helicity of the electron should be changed, according to
eq.(12), to
![]()
If accepted, decide how many laser photons to absorb. To do so,
sum up FINT(*,n,MY,j,l) from n=1 to ![]() until
the sum becomes larger than
until
the sum becomes larger than ![]() . Then,
. Then, ![]() will be the number of photons.
will be the number of photons.
Once ![]() is determined, the photon energy is determined by
is determined, the photon energy is determined by
![]()
where ![]() is another uniform random number. The left hand side is known
for the mesh point of y (i.e., FINT(k,n,MY,j,l)).
Since we approximate
is another uniform random number. The left hand side is known
for the mesh point of y (i.e., FINT(k,n,MY,j,l)).
Since we approximate
![]() by a piecewise linear function of y, the left hand side is a
quadratic function between successive y's.
Thus, inverse interpolation with respect to i by solving a
quadratic equation gives the photon energy to be emitted.
by a piecewise linear function of y, the left hand side is a
quadratic function between successive y's.
Thus, inverse interpolation with respect to i by solving a
quadratic equation gives the photon energy to be emitted.
The helicities of the final photon and electron are calculated from
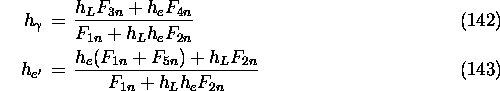
for ![]() . This is done by directly calling a Bessel function routine.
. This is done by directly calling a Bessel function routine.