In the following, ![]() is an approximation in the frame where
the initial electron and laser collide head-on and the electron is
ultra-relativistic.
is an approximation in the frame where
the initial electron and laser collide head-on and the electron is
ultra-relativistic.
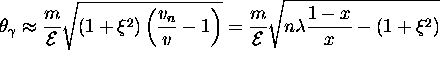
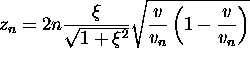
Number of photons per unit time is
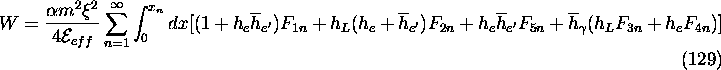
The terms involving ![]() and
and ![]() simultaneously
are ignored, i.e., the correlation of polarization between final particles
is ignored.
The ultra-relativistic approximation has been applied in
the terms related to electron helicity (
simultaneously
are ignored, i.e., the correlation of polarization between final particles
is ignored.
The ultra-relativistic approximation has been applied in
the terms related to electron helicity (![]() and/or
and/or ![]() ). (Note that the electron
helicity is a Lorentz invariant quantity only in the ultra-relativistic limit.)
). (Note that the electron
helicity is a Lorentz invariant quantity only in the ultra-relativistic limit.)
The sum over the final electron and photon helicities gives
![]()
The functions ![]() are defined by
are defined by
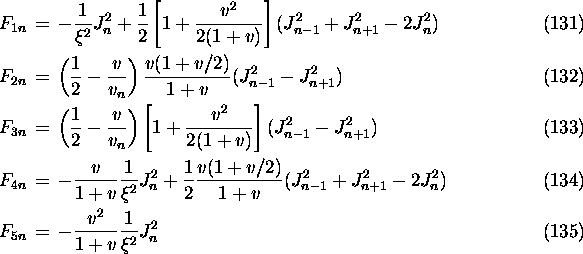
![]() ,
, ![]() ,
, ![]() ,
, ![]() are identical to
are identical to
![]() ,
, ![]() ,
, ![]() ,
, ![]() divided by
divided by ![]() in
Tsai's paper[5], although the expressions in his
paper look much more complicated.
in
Tsai's paper[5], although the expressions in his
paper look much more complicated.
Once x and n are given, the final momentuma are given, in any frame, by
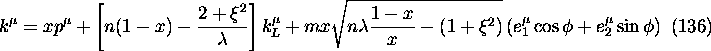
![]()
Here, ![]() is the azimuthal angle in a head-on frame (therefore its
distribution is uniform in [0,
is the azimuthal angle in a head-on frame (therefore its
distribution is uniform in [0,![]() ]) and
]) and
![]() and
and ![]() are given by
are given by
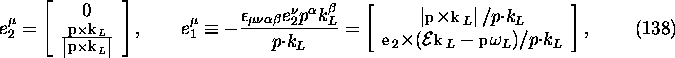
where ![]() is the completely anti-symmetric tensor
(
is the completely anti-symmetric tensor
(![]() ).
These vectors satisfy
).
These vectors satisfy
![]()
The vector ![]() in eq.(139) is ill-defined when
in eq.(139) is ill-defined when ![]() and
and
![]() are colinear in the original frame. In such a case the spatial
part of
are colinear in the original frame. In such a case the spatial
part of ![]() is an arbitrary unit vector perpendicular to
is an arbitrary unit vector perpendicular to ![]() .
.