To treat the Bethe-Heitler , Landau-Lifshitz and the Bremsstrahlung processes, the so-called almost-real-photon approximation, or equivalent photon approximation, or Weizacker-Williams approximation, is employed. An electron is accompanied by virtual photons which look like real photons at ultra-relativistic limit. They interact with on-coming (real or virtual) photons incoherently. Thus, the Bethe-Heitler and Landau-Lifshitz processes above are reduced to the Breit-Wheeler process and the Bremsstrahlung to the Compton process:
' is a virtual photon.
Let the electron energy be 
(
). The number of
virtual photons with energy 
and transverse momentum
is given by
where 
is the fine structure constant. For given ,
the typical transverse momentum is very small, 
,
so that it is not important in collision kinematics but, instead, the
finite transverse extent 
can bring about significant
effects. In the (transverse) configuration space, the above expression
becomes
where 
is the transverse coordinate with respect to the
parent electron, 
, and 
the modified
Bessel function.
The transverse momentum cut off 
(or 
) is somewhat umbiguous. It should depend on the
momentum transfer of the whole process. This dependence is ignored in CAIN
because the virtual photons are generated independently from the
following processes and because it does not much affect the low energy pairs.
The lower limit 
of the integration over is, in our case,
determined by the pair creation threshold.
Let us introduce dimensionless variables 
,
, and 
. The total number of
the virtual photons is given by
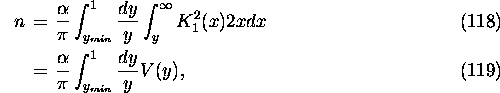
with
When 
, the total number is
where 
is Euler's constant.
At very high energies the number of virtual photons per electron
is O(1), in spite of the small factor 
,
due to the factor 
.
1ex
When Bethe-Heitler and/or Landau-Lifshitz processes are specified by PPINT command, CAIN generates virtual photons in each longitudinal slice at each time step and counts them in the same mesh as that generated by the LUMINOSITY command. The number of macro-virtual photons is somewhat arbitrary. In the present version it is determined such that the weight of the macro-virtual photons is equal to the maximum weight of the electrons in the on-coming beam (not equal to the weight of each parent electron in order to prevent low-weight electrons from generating many photons).
Since the y (energy) spectrum is approximately proportional to
for small y, the spectrum becomes almost flat if one chooses 
as the primary variable. To account for relatively large y too, CAIN
adopts the variable 
instead of y:
Here, c>0 is introduced so that the function 
defined later, is finite.
It is chosen to be 0.2 but is almost arbitrary provided 
.
The maximum is
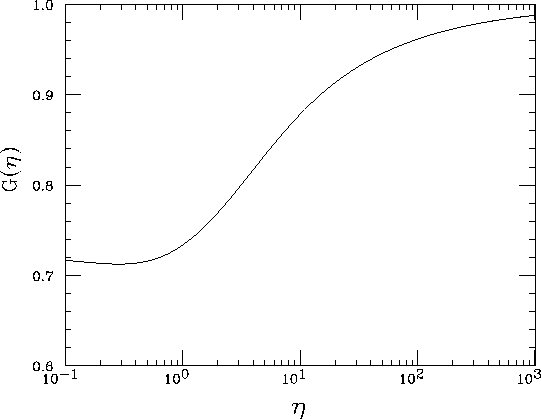
Figure 11: Function defined in eq.(125). It is close to
unity because only large region is important. G(0) is finite and
depends on the
parameter c. G(0)<1 if 
. Here, c=0.2
is adopted.
Now, the spectrum with respect to is
with
For 
, 
and close to 1 except for the small
region which is umimportant in practice. Thus,
For given (or y) the distribution of x is proportional to
dV(x)/V(y) and, therefore, can be random-generated by using inverse function
.
The algorithm is as follows.
, 
and 
is the expected number of macro-virtual photons.
If is not small enough (say, >0.1), divide it by an integer
N and repeat the following steps N times.
.
Reject if 
. Otherwise redefine 
by 
.
, define
and calculate from a table.
Reject if 
. (The probability to be rejected here is small
because G is close to unity.) Otherwise, accept.
.
If LOCAL option is specified, stop here and return
. Otherwise, calculate the value of V(y)
from G using eq.(125).
and solve the equation
with respect to x. This is done by using a table
of inverse function of V.
, 
being the
Compton wave length.
and compute the photon
coordinate
.