The random number generation using the acception-rejection method is applicable when the distribution function is everywhere finite and is most efficient when the function is flat.
Since the function 
is infinite at 
,
the following variable y is introduced in
CAIN instead of the photon energy fraction x in order to make the
distribution function finite and relatively flat.
The number of photons during a time interval 
in the
photon energy range (y,y+dy) is then given by
where
The function 
is
less than or equal to unity for any 
and y.
It is plotted in Fig.7.
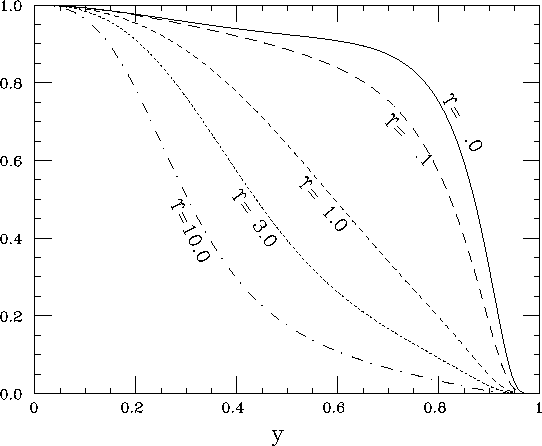
Figure 7: Function
for various values of .
Unpolarized case only.
The photon generation in CAIN proceeds in the following way.
for given field, electron energy, and time interval .
, reject emitting a photon. Otherwise,
. (A polynomial
approximation is used for 
and 
.
The relative error is less than 
.)
, reject emitting a photon.
Otherwise,
is the most time consuming.
The probability to be accepted in (6) is plotted in Fig.8
is given by 
and is plotted
as a function of . One finds the probability is very high
for any owing to the choice of the variable y.
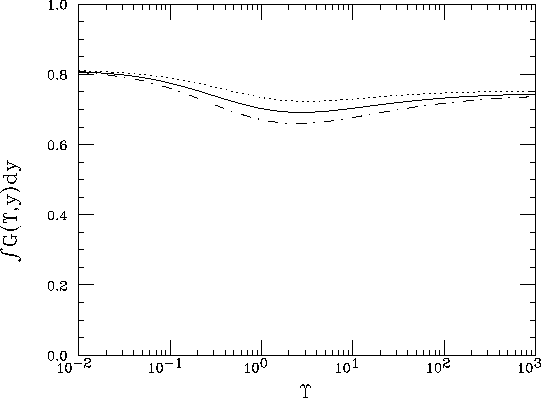
Figure 8: The acception probability in the step (6) as a function of
. The solid line is the unpolarized case
The dot-dash and dotted lines are polarized cases with
= 1 and -1, respectively.