In order to investigate our method quantitatively by taking into
account all beam-beam effects, which include beam disruption, the
horizontal crossing angle, the vertical displacement between two
beams, transverse rotations for flat beams and the energy and angular
distributions of created pairs etc., we must rely on Monte-Carlo
simulations by using ABEL, although the principal dynamics can be well
described analytically by an approximation of the elliptic cylinder,
as demonstrated in the previous section. A detailed explanation of
ABEL can be found in [6, 4]. As an example of a future
linear collider we consider JLC-I[1], whose parameters
relevant to the simulation are given as follows: the beam energy
(
) is 250GeV and the intensity (N) is 
/bunch;
Gaussian beams with 
nm,
m, the horizontal crossing angle
mrad and the luminosity 
cm
sec
with 72 bunches/pulse at the frequency of 150 Hz.
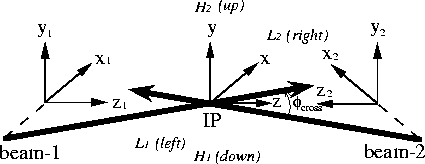
Figure 2:
Coordinate system used in ABEL, where 
and z
are collinear. The trajectories of the beam-centers are indicated by
the long/thick arrows.
We first define the coordinate system used in ABEL.
There are three kinds of coordinate systems shown in Fig.2.
Two of them, 
and 
, move together
with beam-1 (positrons) and beam-2 (electrons), respectively.
The former is a left-handed system, while the latter is a
right-handed system. The third one, (x,y,z), is the rest frame at
IP. All three coordinates are collinear in the z-direction. In
the presence of crossing, the origins of the moving systems are
shifted from the centers of the beams, except in the 
- and 
-
directions, as shown in Fig.2. The crossing angles of two
beams are +4mrad, each in the directions of 
and 
, that
is 8mrad (
) between them. Since we expect a large
asymmetry in the azimuthal angular distribution of the deflected
particles, especially in the vertical-horizontal asymmetry for flat
beams, as explained in the previous section, we define 4 azimuthal
angular regions in Fig.2 (
and 
)
corresponding to left, right, down and up, respectively, as seen from
the upstream of beam-2.
The 
pairs are generated from three processes (BH, BW and
LL), where the energies of the particles are more than 5 MeV; they are
tracked with all of the effects during a beam-beam crossing by
ABEL[4]. After the crossing, the azimuthal angular
distribution is plotted for particles whose energies (
) and
deflection angles (
) are more than 100 MeV and 20 mrad,
respectively, in Fig.3 (a),
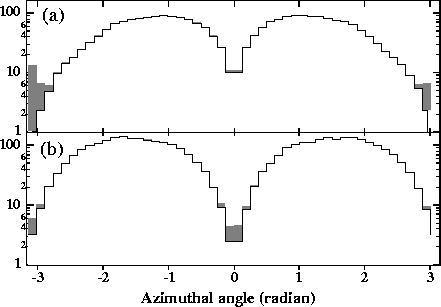
Figure 3:
(a) Azimuthal angular distribution of deflected electrons
and positrons(
MeV, 
) for
JLC-I. The shaded area corresponds to that of those positrons which
are oppositely charged particles as that of the oncoming beam. (b)
The same as (a) except for a zero horizontal crossing angle, i.e. for
a head-on collision. The vertical scale is the number of particles
per single-bunch crossing.
which is compared to the case of a head-on collision, i.e. the zero
horizontal crossing angles shown in Fig.3 (b).
Hereafter, we always show the azimuthal angles measured downstream
from beam-1, that is, those of the particles deflected by beam-2,
since the distributions are symmetrical at both sides of IP for the
same parameters of the two beams. As can be clearly seen in
Fig.3, electrons of the pairs, which have the same
charge as those of beam-2, are strongly deflected in the vertical
direction, while the positrons show only a moderate suppression in the
horizontal plane, as indicated by the shaded area in this figure. We
can also see the effect of the 8mrad crossing with a tendency of
deflecting more to the right. This shows a general feature, that is,
when particles have a finite initial angle they are deflected more in
this direction. The crossing angle generates a horizontal
displacement (
) uniformly over the particles at a very
early stage of their deflections. The certain displacement of
is the origin of this feature, as mentioned in the
previous section.
Since the created particles have inherent scattering angles
(
) of typically 
, where 
is the
electron mass, an effect due to these angles is also expected. It
has been found to produce a deeper depletion in the horizontal
direction than speculated in the previous section, where the inherent
angle was neglected. F(0) (also 
) is now nearly
proportional to 1/R rather than to 
in
Eq.(13), as can be seen in Fig.4.
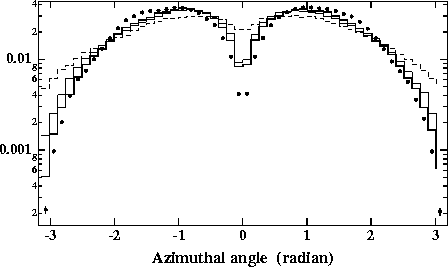
Figure 4:
Azimuthal angular distributions of deflected electrons
(
MeV, 
), whose charges are the same as
that of beam-2 for JLC-I with nominal parameters (solid circles)
together with three cases (
= 
(solid
line), 
(dotted one) and 
(dashed
one)) in which the other beam parameters are the same as those of the
nominal beam. The distributions were normalized by the total number
of electrons in them.
In this figure the azimuthal angular distribution for the nominal
JLC-I parameters is compared with three cases ( = 
and ), where the
other parameters are the same as the nominal ones and only those
electrons of MeV and are plotted in order
to see the depletion more clearly as a function of .