


Next: Helix to Straight Line
Up: Track Linking
Previous: Track Linking
Before combining track segments, we move their pivots to a common
point which can be arbitrarily chosen.
We should also correct the track parameters for energy loss and
multiple scattering beforehand
so that they represent the track parameters for the
original track.
Then the total 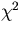 for the combined track is then
given by
for the combined track is then
given by
| 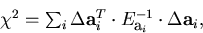 |
(22) |
where
and 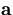 is the track parameter vector for the original track,
is the track parameter vector for the original track,
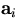 is that determined by i-th tracking device,
and
is that determined by i-th tracking device,
and 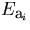 is the corresponding error matrix.
Since this is quadratic in
is the corresponding error matrix.
Since this is quadratic in 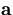 , the minimization
of the
, the minimization
of the 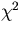 can be carried out
analytically by a single matrix inversion:
can be carried out
analytically by a single matrix inversion:
| 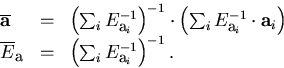 |
(23) |
The above formulae tell us that the track linking in the parameter space is a
simple averaging process![[*]](foot_motif.gif) .
.
Keisuke Fujii
12/4/1998
![]() for the combined track is then
given by
for the combined track is then
given by
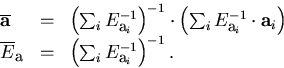
![[*]](foot_motif.gif) .
.