In order to see the effects of the choice of the ![]() cut, we have studied Higgs production in
cut, we have studied Higgs production in
![]() and
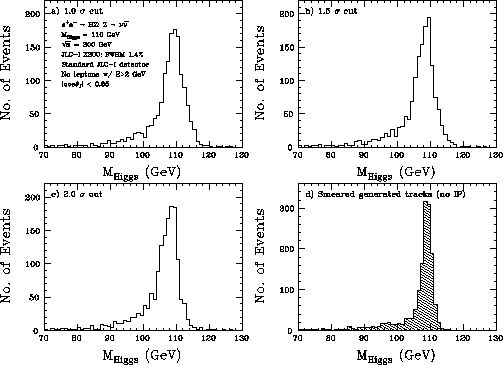
and ![]() .Figs.3.4-a) to -c) plot reconstructed Higgs mass distributions
with three different values of
.Figs.3.4-a) to -c) plot reconstructed Higgs mass distributions
with three different values of ![]() cut:
1.0-
cut:
1.0-![]() , 1.5-
, 1.5-![]() , and 2.0-
, and 2.0-![]() .These three figures should be compared to each other as well as to
Fig.3.4-d) which is the mass distribution with smeared
generated tracks.
We can see that when n is too small, we have a upward tail
in the distribution because of undeleted clusters due to charged
hadrons. On the other hand, a too large n misdeletes
clusters due to neutral hadrons and consequently lowers the
center value of the mass peak.
.These three figures should be compared to each other as well as to
Fig.3.4-d) which is the mass distribution with smeared
generated tracks.
We can see that when n is too small, we have a upward tail
in the distribution because of undeleted clusters due to charged
hadrons. On the other hand, a too large n misdeletes
clusters due to neutral hadrons and consequently lowers the
center value of the mass peak.
 |