New formula for hadron shower

According to Dr. Yoshiaki Fujii, following formula is as a lateral distribution of hadron shower.

$$G(r) = p_1 \exp^{-r/p_2} + p_3 \exp^{-(r/p_4)^2}$$ (2)

where r is radius from the particle entrance and typical value for parameters are (p₁,p₂,p₃,p₄)=(3.6, 13.4, 6.4, 2.47).

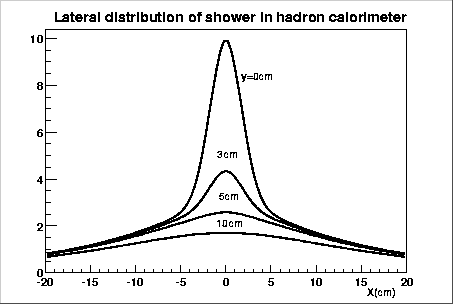
Fig. 1 shows the function, G(r), for y=0, 3, 5, and 10 cm, as a function of X.

  

Figure 1: A function of hadron shower distribution, G(r). Plotted for y=0, 3, 5, and 10 cm, as a function of x coordinate.

In the Fig. 2, the lateral distribution of hadron shower used in the current quick simulator and the one given by Eq. 2 are compared. The function G(r) is a function of radius, while the function F(x)defined in Eq. 1 is the distribution projected on x axis, we integrated G(r) with respect to y when they are compared in the Fig. 2. G(r) is the signal density in small area $r dr d\phi$. By change of the variable, $r dr d\phi = dx dy$. Therefore,

$$P(x)\equiv \int G(r) dy$$ (3)

where $r=\sqrt{x^2+y^2}$.

  

Figure 2: Lateral distribution of hadron shower used in the current quick simulator compared with the distribution given by G(r).

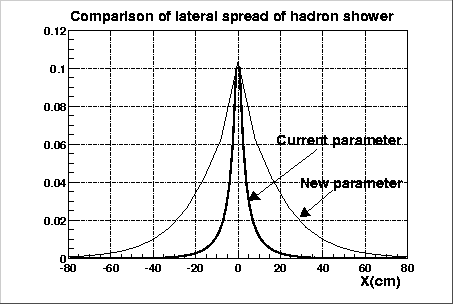From the Fig. 2, it is found that the lateral distribution of current quick simulator is about five times narrower than those given by the function, G(r). However, shape seems to be equal. Therefore, we fit the projected distribution provided by Eq. 2 by the function F(x) given by Eq. 1. The fit result are shown in the Fig. 3.

  

Figure 3: The fit to the shower shape. The data points are those calculated from Eq. 2.

In the JLC weekly meeting in 14 January, 2000, it was pointed out that the integration of Eq. 2 as described above is not correct. Correct treatment needs further study. For a time beeing, continue study using old method and old parameters.