// @(#)root/geom:$Name:  $:$Id: TGeoShape.cxx,v 1.8 2003/02/07 13:46:47 brun Exp $
// Author: Andrei Gheata   31/01/02

/*************************************************************************
 * Copyright (C) 1995-2000, Rene Brun and Fons Rademakers.               *
 * All rights reserved.                                                  *
 *                                                                       *
 * For the licensing terms see $ROOTSYS/LICENSE.                         *
 * For the list of contributors see $ROOTSYS/README/CREDITS.             *
 *************************************************************************/

////////////////////////////////////////////////////////////////////////////////
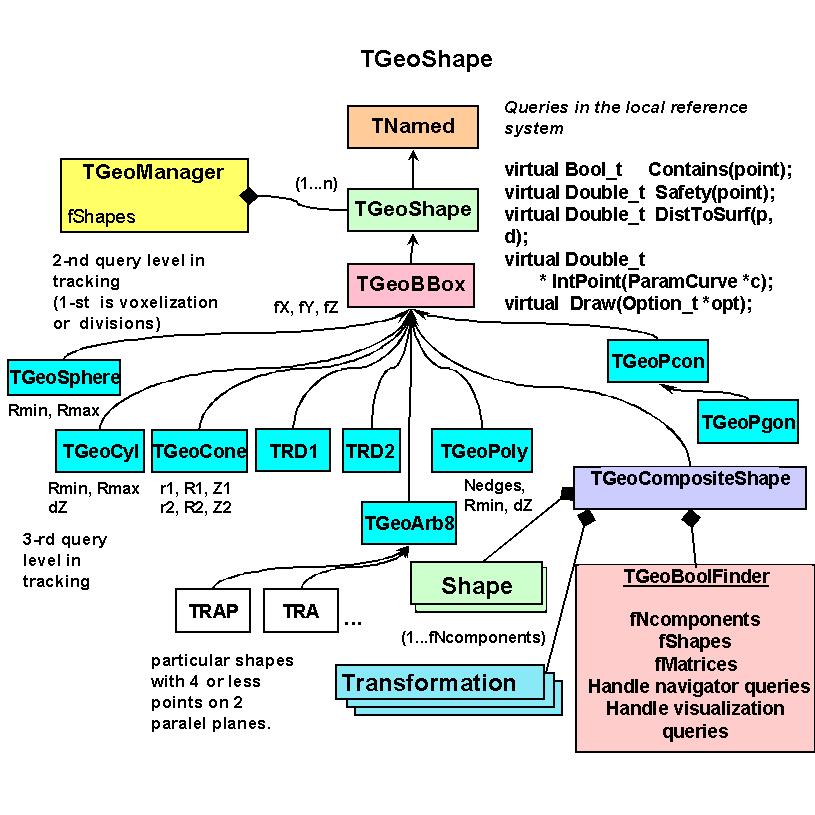
// TGeoShape - base class for all geometrical shapes. Abstract functionality
//   regarding point and segment classification has to be implemented by classes
//   that inherits from it.
//
//
//
/*

*/
//
#include "TObjArray.h"

#include "TGeoMatrix.h"
#include "TGeoManager.h"
#include "TGeoVolume.h"
#include "TGeoShape.h"
#include "TVirtualGeoPainter.h"


/*************************************************************************
 * TGeoShape - package description
 *
 * Creating shapes
 *================
 *   Shape objects embeed only the minimum set of parameters that are fully
 * describing a valid physical shape. For instance, a tube is represented by
 * its half length, the minimum radius and the maximum radius. Shapes are used
 * togather with media in order to create volumes, which in their turn 
 * are the main components of the geometrical tree. Volumes may contain other
 * positioned volumes inside, which are called nodes. Each component in this 
 * structure : media, shapes and volumes (except nodes) are replicable (one
 * instance of an object can be used in several other combinations). 
 *    It is highly recomendable to use replicas as more as possible when volumes
 * have different media but the same shape. One will never have to create 
 * an instance of the TGeoShape class, but only the one for specific shapes :
 *
 *   TGeoBBox *box = new TGeoBBox(halfX, halfY, halfZ);
 *   TGeoTube *tub = new TGeoTube(rmin, rmax, halfZ);
 *   ...  (see each specific shape constructors)
 *
 *   Sometimes it is much easier to create a volume having a given shape in one 
 * step, since shapes are not direcly linked in the geometrical tree but volumes 
 * are :
 *
 *   TGeoVolume *vol_box = gGeoManager->MakeBox("BOX_VOL", "mat1", halfX, halfY, halfZ);
 *   TGeoVolume *vol_tub = gGeoManager->MakeTube("TUB_VOL", "mat2", rmin, rmax, halfZ);
 *   ...  (see MakeXXX() utilities in TGeoManager class)
 *
 *   Volumes can be assembled also from pieces :
 *  
 *   TGeoVolume *vol = new TGeoVolume(name, ptr_shape, ptr_medium);  
 *
 * Point and segment classification
 *=================================
 *   The main functionalities of a shape is finding if a given point is contained 
 * or not or if an oriented segment crosses or not the shape. Further functionalities
 * are : computing the normal to the shape surface at intersection point and finding
 * the minimim distance from a point to it.
 *   These algorithms can be called by user only if the checked point/segment is
 * converted to the local reference frame. Mainly they are used by the global
 * point/segment classification algorithms of TGeoManager class.
 *   See also : TGeoManager::FindNode() , TGeoManager::FindNextBoundary()
 *
 *  Classification of arbitrary curves (e.g. helixes) w.r.t shapes is not 
 * implemented yet.  
 *
 *************************************************************************/

const Double_t TGeoShape::kRadDeg = 180./TMath::Pi();
const Double_t TGeoShape::kDegRad = TMath::Pi()/180.;
const Double_t TGeoShape::kBig = 1E30;

ClassImp(TGeoParamCurve)
ClassImp(TGeoShape)

//-----------------------------------------------------------------------------
TGeoShape::TGeoShape()
{
// Default constructor
   fShapeId = 0;
   if (!gGeoManager) {
      gGeoManager = new TGeoManager("Geometry", "default geometry");
      // gROOT->AddGeoManager(gGeoManager);
   }
//   fShapeId = gGeoManager->GetListOfShapes()->GetSize();
//   gGeoManager->AddShape(this);
}
//-----------------------------------------------------------------------------
TGeoShape::TGeoShape(const char *name)
          :TNamed(name, "")
{
// Default constructor
   fShapeId = 0;
   if (!gGeoManager) {
      gGeoManager = new TGeoManager("Geometry", "default geometry");
      // gROOT->AddGeoManager(gGeoManager);
   }
   fShapeId = gGeoManager->GetListOfShapes()->GetSize();
   gGeoManager->AddShape(this);
}
//-----------------------------------------------------------------------------
 TGeoShape::~TGeoShape()
{
// Destructor
   if (gGeoManager) gGeoManager->GetListOfShapes()->Remove(this);
}
//-----------------------------------------------------------------------------
 const char *TGeoShape::GetName() const
{
   if (!strlen(fName)) {
      return ((TObject *)this)->ClassName();
   }
   return TNamed::GetName();
}
//-----------------------------------------------------------------------------
 Int_t TGeoShape::ShapeDistancetoPrimitive(Int_t numpoints, Int_t px, Int_t py) const
{
   TVirtualGeoPainter *painter = gGeoManager->GetGeomPainter();
   if (!painter) return 9999;
   return painter->ShapeDistancetoPrimitive(this, numpoints, px, py);
}
//-----------------------------------------------------------------------------
 Double_t TGeoShape::ClosenessToCorner(Double_t *point, Bool_t in,
                                 Double_t *vertex, Double_t *normals, Double_t *cldir)
{
// Static method returning distance to closest point of a corner. The corner is 
// defined by vertex and normals to the 3 planes (in order X, Y, Z - norm[9]).
// also return unit vector pointing to this
  
   Double_t safe[3];  // closest distances to the 3 planes
   Double_t dvert[3]; // vector from vertex to point
   Int_t snorm = -1;
   Double_t close = 0;                                 
   memset(&safe[0], 0, 3*sizeof(Double_t));
   memset(cldir, 0, 3*sizeof(Double_t));
   Int_t i, j;
   for (i=0; i<3; i++)
      dvert[i]=point[i]-vertex[i];
   for (i=0; i<3; i++) {
      for (j=0; j<3; j++)
         safe[i]+=dvert[j]*normals[3*i+j];
   }   
   // point is inside
   if (in) {
      snorm = TMath::LocMax(3, &safe[0]);
      close = -safe[snorm];
      // check if point was outside corner
      if (close<0) return kBig;
      memcpy(cldir, &normals[3*snorm], 3*sizeof(Double_t));
      return close;   
   }
   // point is outside
   UInt_t nout=0;
   for (i=0; i<3; i++) {
      if (safe[i]>0) { 
         snorm = i;
         close = safe[i];
         nout++;
      }   
   }   
   // check if point is actually inside the corner (no visible plane)
   if (!nout) return kBig;
   if (nout==1) {
      // only one visible plane
      memcpy(cldir, &normals[3*snorm], 3*sizeof(Double_t));
      return close;
   }   
   if (nout==2) {
   // two faces visible
      Double_t calf = 0;
      Double_t s1=0;
      Double_t s2=0;
      for (j=0; j<3; j++) {
         if (safe[j]>0) {
            if (s1==0) s1=safe[j];
            else       s2=safe[j];
            continue;
         }   
         for (Int_t k=0; k<3; k++) 
            calf += normals[3*((j+1)%3)+k]*normals[3*((j+2)%3)+k]; 
      }
      close=TMath::Sqrt((s1*s1 + s2*s2 + 2.*s1*s2*calf)/(1. - calf*calf));
      return close;
   }   
   
   if (nout==3) {
   // an edge or even vertex more close than any of the planes
   // recompute closest distance
      close=0;
      for (i=0; i<3; i++) {
         if (safe[i]>0) close+=dvert[i]*dvert[i];
      } 
      close = TMath::Sqrt(close);
      for (i=0; i<3; i++)
         cldir[i] = dvert[i]/close;
      return close;           
   }
   return close; // never happens
}   

//-----------------------------------------------------------------------------
 Double_t TGeoShape::DistToCorner(Double_t *point, Double_t *dir, Bool_t in, 
                                 Double_t *vertex, Double_t *norm, Int_t &inorm)
{
// Static method to compute distance along a direction from inside/outside point to a corner.
// The corner is  defined by its normals to planes n1, n2, n3, and its vertex. 
// Also compute distance to closest plane belonging to corner, normal to this plane and
// normal to shape at intersection point.

// iact=0 :
 
//   printf("checking corner : %f %f %fn", vertex[0], vertex[1], vertex[2]);
//   printf("normx : %f %f %fn", norm[0], norm[1], norm[2]);
//   printf("normy : %f %f %fn", norm[3], norm[4], norm[5]);
//   printf("normz : %f %f %fn", norm[6], norm[7], norm[8]);
   Double_t safe[3];  // closest distances to the 3 planes
   Double_t dist[3];  // distances from point to each of the 3 planes along direction
   Double_t dvert[3]; // vector from vertex to point
   Double_t cosa[3];  // cosines of anles between direction and each normal
   Double_t snxt = kBig;
   inorm = -1;
   memset(&safe[0], 0, 3*sizeof(Double_t));
   memset(&cosa[0], 0, 3*sizeof(Double_t));
   Int_t i, j;
   
   for (i=0; i<3; i++) {
      dvert[i]=point[i]-vertex[i];
      dist[i] = kBig;
   }   
//   printf("dvert : %f %f %fn", dvert[0], dvert[1], dvert[2]);
   for (i=0; i<3; i++) {
      for (j=0; j<3; j++) {
         safe[i]+=dvert[j]*norm[3*i+j];
         cosa[i]+=dir[j]*norm[3*i+j];
      }   
   }   
   // point is inside
   if (in) {
      if (safe[0]>0) return kBig;
      if (safe[1]>0) return kBig;
      if (safe[2]>0) return kBig;
      for (i=0; i<3; i++) 
         if (cosa[i]>0) dist[i]=-safe[i]/cosa[i];
      inorm = TMath::LocMin(3, &dist[0]);
      snxt = dist[inorm];
      return snxt;
   }
   // point is outside
   UInt_t npos=0;
   UInt_t nout=0;
   UInt_t npp=0;
   Double_t dvirt = kBig;
   snxt = 0;
   
   for (i=0; i<3; i++) {
      if (safe[i]>0) nout++;
      if (cosa[i]!=0) 
         dist[i]=-safe[i]/cosa[i];
      if (dist[i] < 0) continue;   
      npos++;
      if (safe[i]>0) {
      // crossing with visible plane
         npp++;
         if (snxt<dist[i]) {
         // most distant intersection point is the real one
            inorm = i;
            snxt = dist[i];
         }
      } else {
      // crossing with invisible plane      
            // compute distance to closest virtual intersection
            dvirt=TMath::Min(dvirt, dist[i]);
      }   
   }
//   printf("  safe : %f %f %f nout=%in", safe[0], safe[1], safe[2], nout);
//   printf("  dist : %f %f %fn", dist[0], dist[1], dist[2]);
//   printf("  dist to next : %fn", snxt);
//   printf("  closest virtual : %fn", dvirt); 
//   printf("  inorm=%i snorm=%in", inorm, snorm);
//   printf("  nout=%i npos=%i npp=%in", nout, npos, npp);
   // select distance to closest plane
   if (!nout) {
   // point is actually inside the corner (no visible plane)
      inorm = -1;
      return kBig;
   }
   if (nout==1) {
   // only one face visible
      if (npp!=1 || snxt>dvirt)  {
         inorm = -1;
         return kBig;
      }
      return snxt;
   }      
   if (!npos) {
   // ray does not intersect any plane
      inorm = -1;
      return kBig;
   }   
   if (npp!=nout) {
   // ray ray does not intersect all visible faces
      inorm = -1;
      return kBig;
   }   
   if (snxt>dvirt) {
   // intersection with invisible plane closer than with real one -> no real intersection
//      close=kBig;
      inorm = -1;
      return kBig;
   }   
   return snxt;
}
//-----------------------------------------------------------------------------
 Int_t TGeoShape::GetVertexNumber(Bool_t vx, Bool_t vy, Bool_t vz)
{
// get visible vertex number for : box, trd1, trd2, trap, gtra, para shapes   
   Int_t imin, imax;
   if (!vz) {
      imin = 0;
      imax = 3;
   } else {
      imin = 4;
      imax = 7;
   }   
   if (!vx)
      imax=imin+1;
   else
      imin = imax-1;
   if(!vy) {
      if (!vx) return imin;
      return imax;
   }
   if (!vx) return imax;
   return imin;
}               
//-----------------------------------------------------------------------------
 Double_t TGeoShape::SafetyPhi(Double_t *point, Bool_t in, Double_t c1, Double_t s1, Double_t c2, Double_t s2)
{
// Static method to compute safety w.r.t a phi corner defined by cosines/sines
// of the angles phi1, phi2.
   Double_t saf1 = kBig;
   Double_t saf2 = kBig;
   if (point[0]*c1+point[1]*s1 >= 0) saf1 = -point[0]*s1 + point[1]*c1;
   if (point[0]*c2+point[1]*s2 >= 0) saf2 =  point[0]*s2 - point[1]*c2;
   if (in) {
      if (saf1<0) saf1=kBig;
      if (saf2<0) saf2=kBig;
      return TMath::Min(saf1,saf2);
   }
   if (saf1<0 && saf2<0) return TMath::Max(saf1,saf2);
   return TMath::Min(saf1,saf2);
}