Top Quark Physics
Overview of Physics at tt-bar Threshold
Theoretical Background
The top quark with a mass in excess of 150 GeV has a very large decay width:
m_t (GeV) Gamma_t (GeV)
-----------------------------
100 0.09
125 0.37
150 0.81
175 1.42
200 2.23
-----------------------------which makes the top quark unique compared to the other quarks.
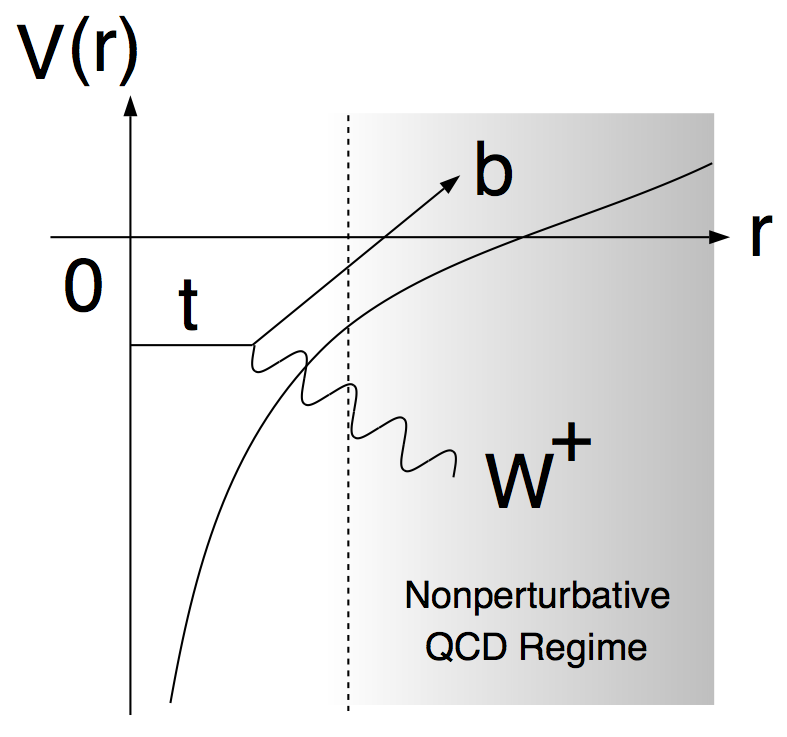
The top and the anti-top pair-created at r=0 thus decay before entering the non-perturbative regime of QCD. Because of this, the production cross section can be reliably calculated with perturbative QCD, as first pointed out by Fadin and Khoze.
We can thus carry out clean tests of perturbative QCD and precision measurements of the strong coupling constant (αs). More importantly, since the QCD contribution is unambiguously calculable, other smaller effects such as the Higgs boson exchange contribution may be extractable.
The leading QCD contribution comes from the multiple exchange of Coulombic gluons which is possible because the top and the anti-top are slow near threshold and stay close to each other.
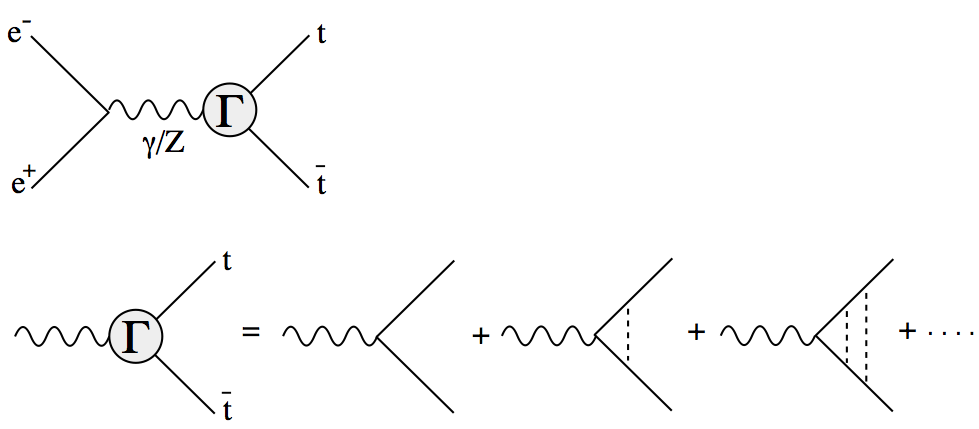
The threshold correction factor Γ in the figure above satisfies the Bethe-Salpeter equation which reduces to Schroedinger's equation
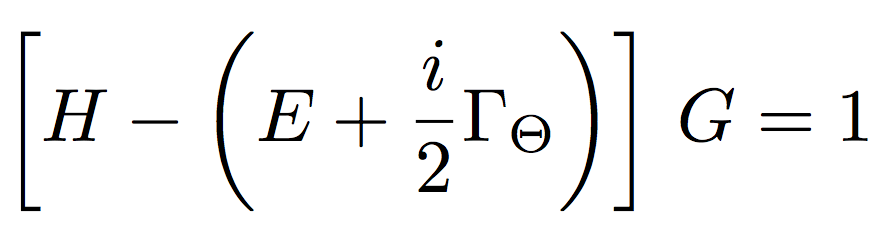
in the nonrelativistic limit. The operator G is related to the threshold correction factor Γ through
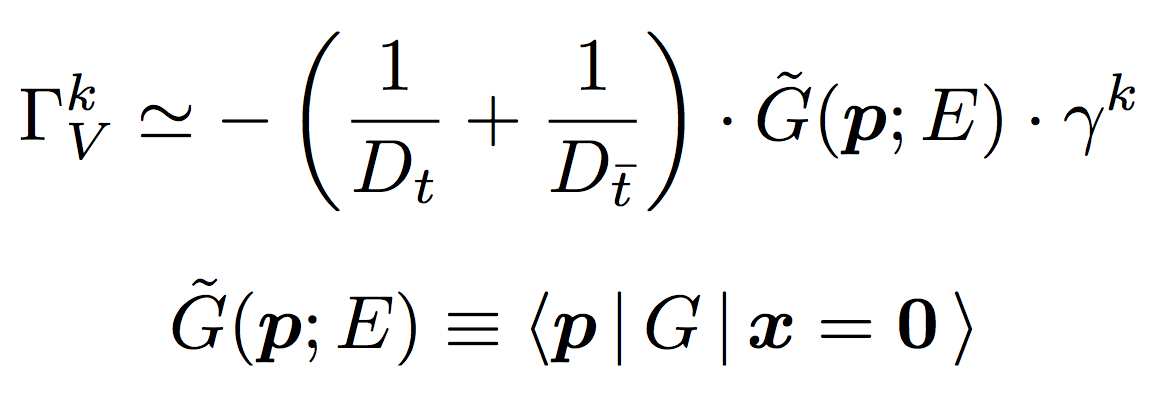
for the vector part corresponding to S-wave resonances and through
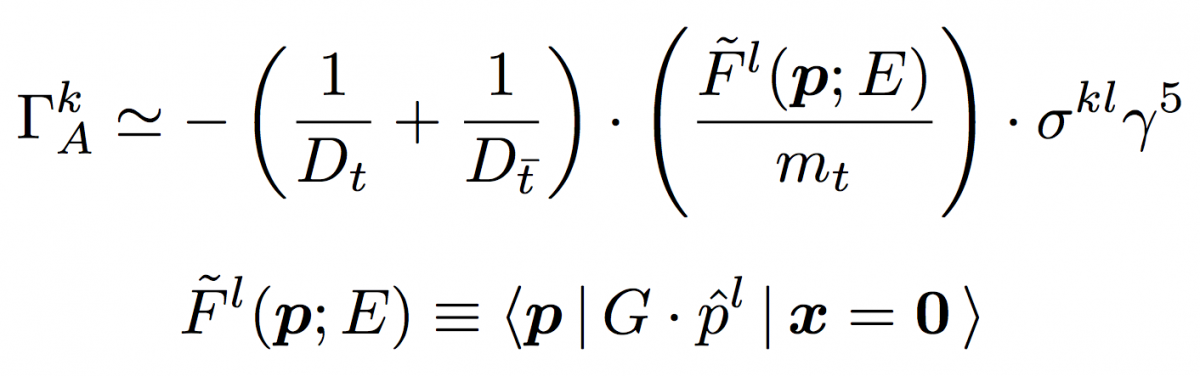
for the axial vector part corresponding to P-wave resonances, where Dt and Dt are the top and the anti-top propagator factors.
Essentially all the t-tbar physics near threshold are contained in the threshold correction factor Γ or G, which depends on the top momentum (P), the energy measured from the threshold (E), the strong coupling constant (αs), the top width (Γt), and, when the Higgs exchange contribution is sizable, the Higgs mass (mH) and the normalized top Yukawa coupling (βH).
Now the question is how to measure G. We can measure the total cross section:
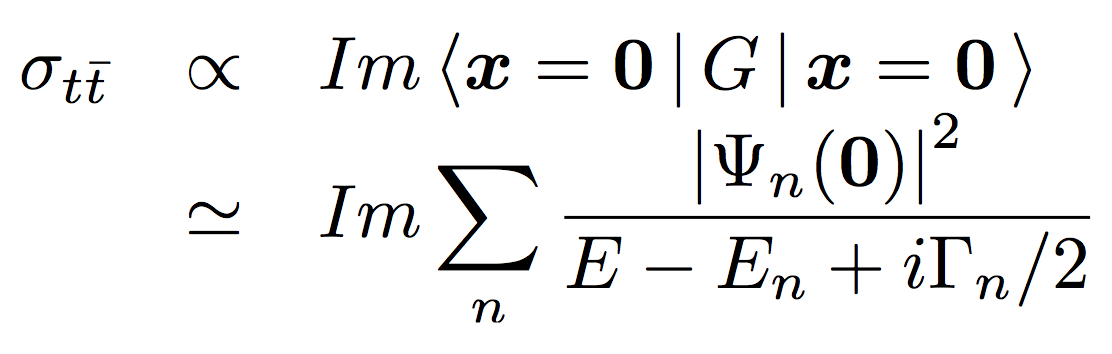
where n runs over resonances. We can see that the measurement of the total cross section is sensitive only to the absolute value of the coordinate-space wave function at the origin.
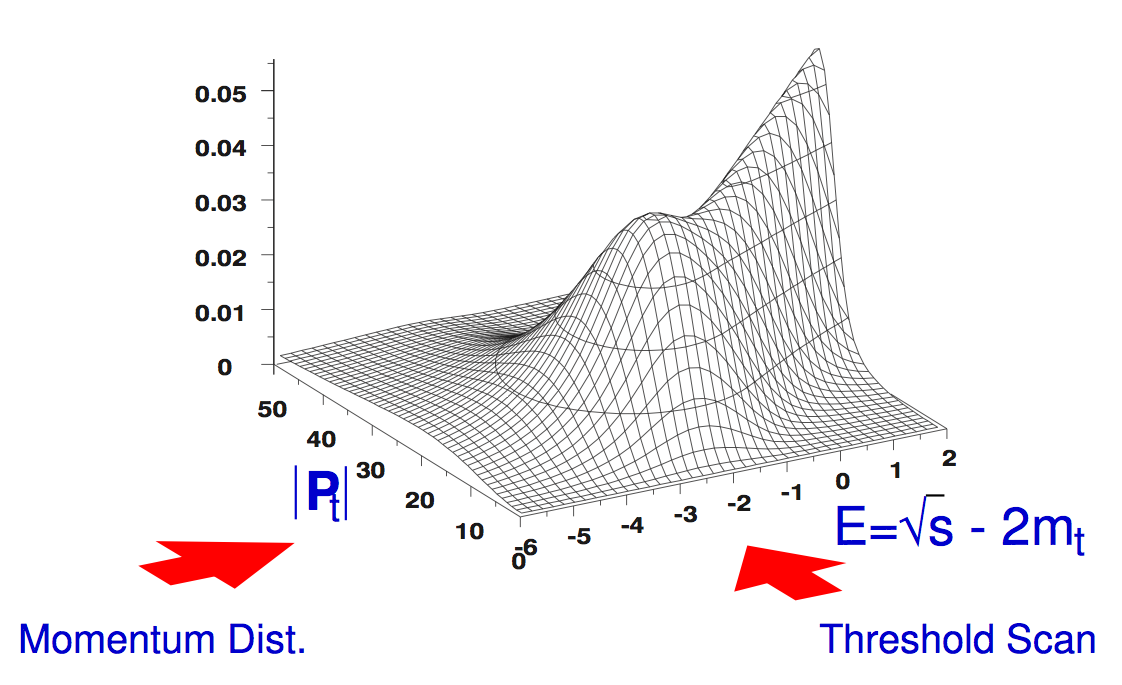
On the other hand, the differential cross section (top momentum distribution) directly reflects the shape of the momentum-space wave functions:
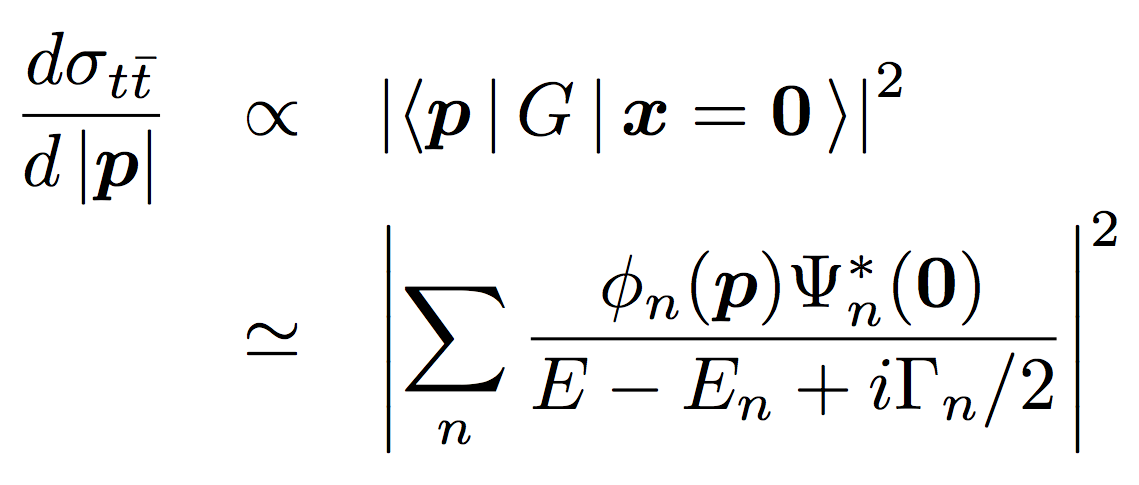
Notice that this is the first opportunity to measure the wave functions of quarkonia, since the lighter quarkonia decay via annihilation and the information on their constituent quark momenta is lost; the top momentum can be measured as the sum of the momenta of daughters (b-quark, and qq pair from W).
We can measure the total cross section through an energy scan of the threshold region, while the top momentum distribution through the reconstruction of the top or anti-top decays to the three jets.