トップ・クォークの物理
トップ対しきい値領域での物理の概観
理論的背景
質量が 150 GeV を越える重いトップクォークは大きな崩壊巾を持っている。
m_t (GeV) Gamma_t (GeV)
-----------------------------
100 0.09
125 0.37
150 0.81
175 1.42
200 2.23
-----------------------------
この大きな崩壊巾は、トップ・クォークを他のクォークにない特徴的な物にしている。
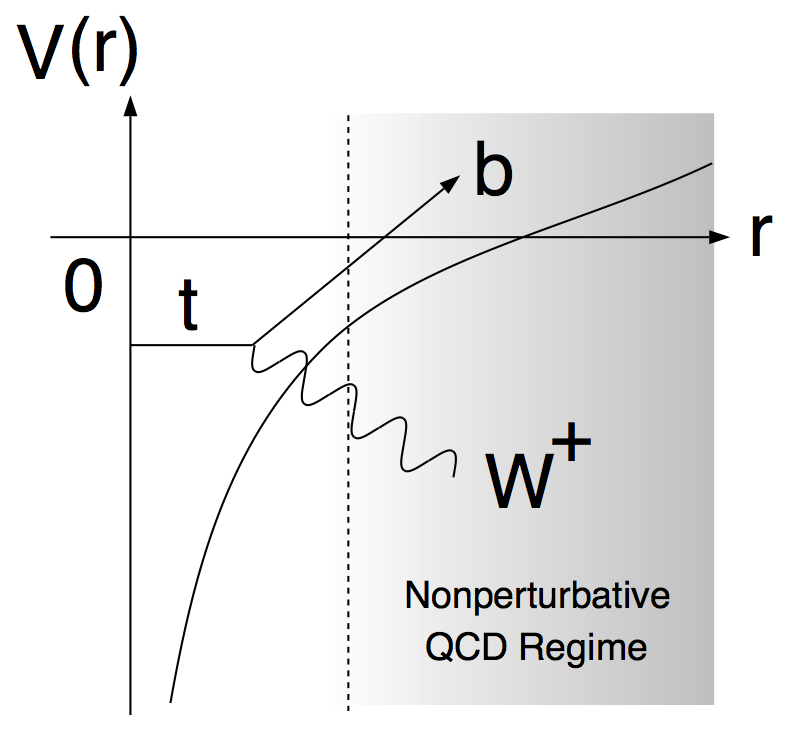
この大きな崩壊巾により原点で生成されたトップ・反トップ対は QCD の非摂動領域に到達する前に崩壊する。 そのおかげで、Fadin と Khoze により最初に指摘されたように、 トップ・反トップ対の生成断面積の摂動 QCD による信頼できる評価が出来る。
こうして、摂動 QCD の明快な検証や、強い相互作用の結合定数 (αs) の精密測定が可能となる。 さらに重要なことは、QCD の寄与が不定性無く計算できることによって、他のより小さい効果(例えばヒッグス交換の寄与)を引き出す可能性が開けたことである。
最も大きな QCD の寄与は、クーロン的なグルーオンの多重交換から来る。 これは、しきい値領域ではトップ・反トップ対はゆっくり走るので、比較的長い間、お互いに近くにいるためである。
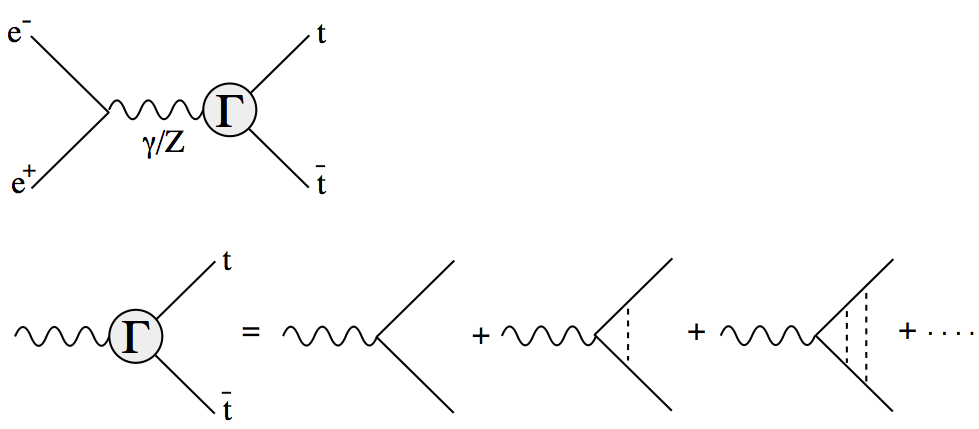
図中で Γ はしきい値補正因子で、Bethe-Salpeter 方程式を満足する。 この方程式は、非相対論近似で次の Schroedinger 方程式に帰着する。
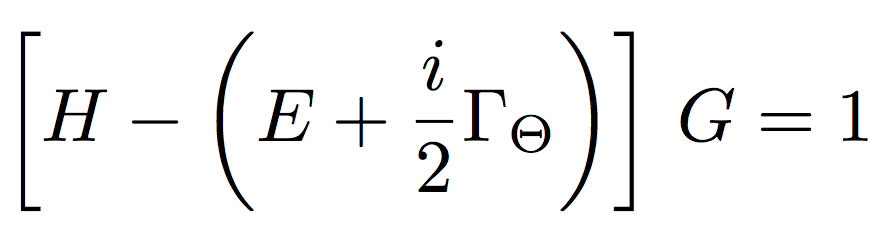
ここで、演算子 G はしきい値補正因子 Γ と次の関係で結ばれている。 つまり、S-波に対応するベクトル部分については
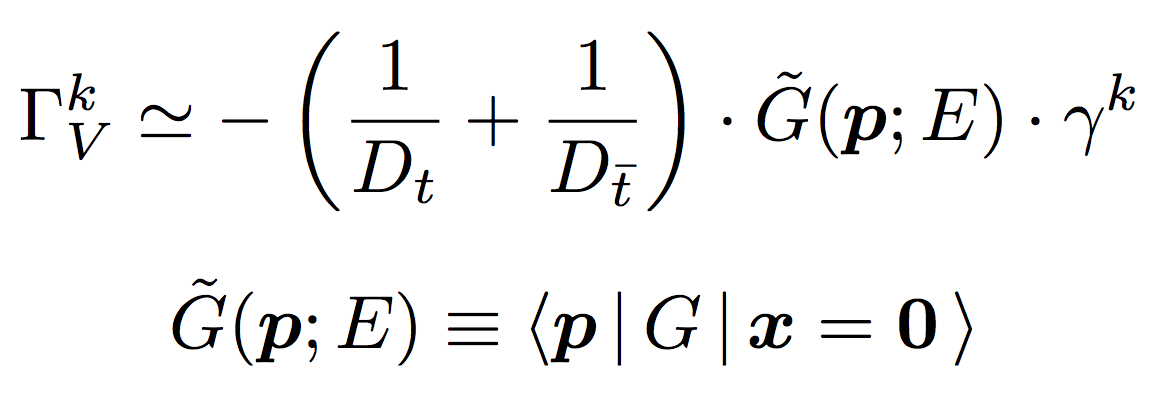
また、P-波に対応する軸性ベクトル部分については
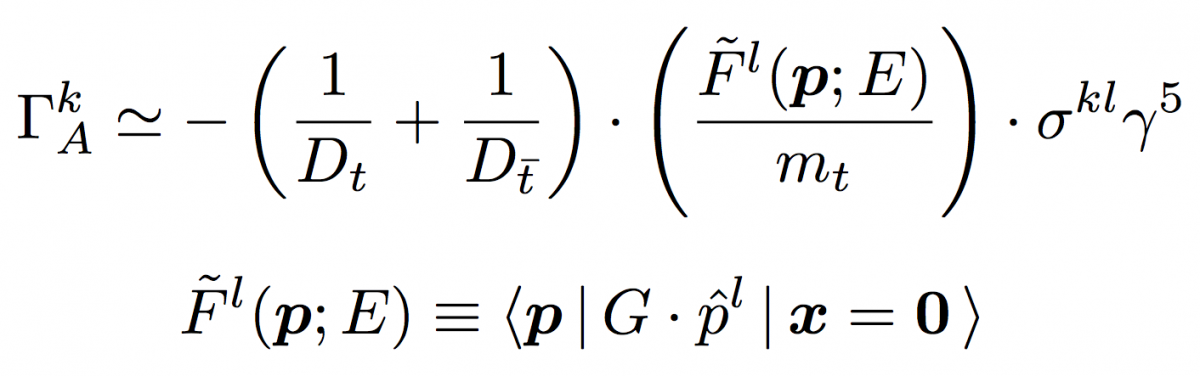
である。 また、Dt および Dt は、トップおよび反トップの伝搬関数因子である。
本質的に、しきい値領域でのトップ・反トップ対生成の物理の全てがこの補正因子 Γ あるいは G に含まれていると言って良い。 Γ あるいは G は、トップの運動量 (P)、 しきい値から測った重心系エネルギー (E)、 強い相互作用の結合定数 (αs)、 トップの崩壊巾 (Γt)、 そして、ヒッグス交換の寄与が重要な場合には、 ヒッグスの質量 (mH)、 規格化したトップのヒッグスへの湯川結合定数 (βH) で決まる。
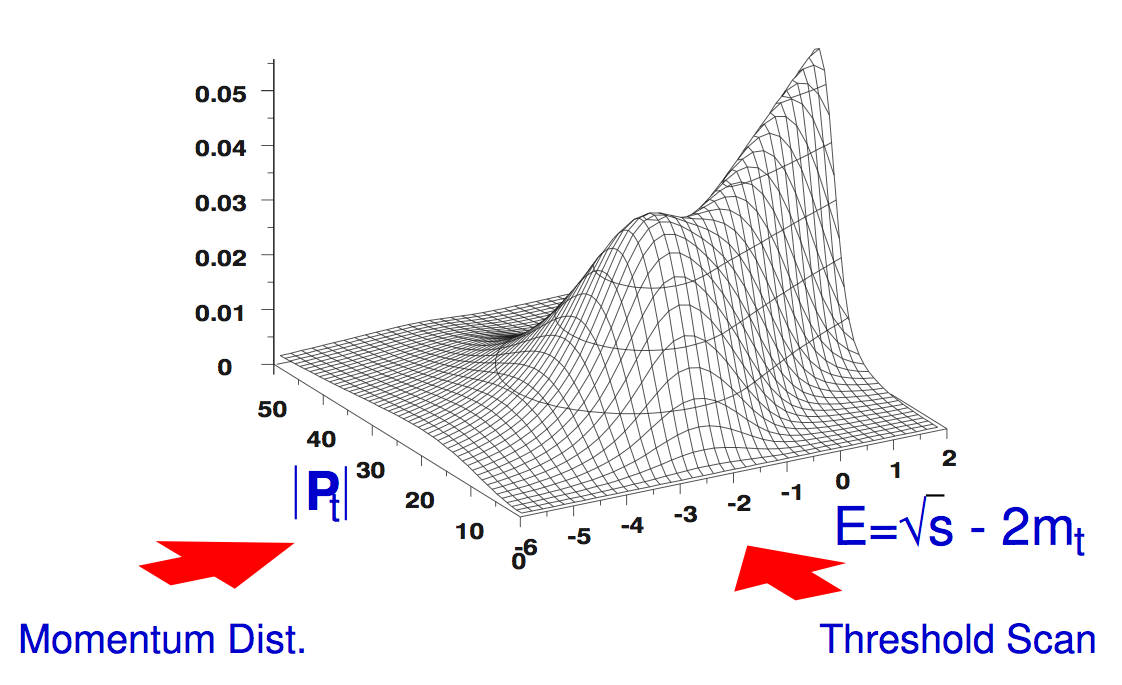
そこで問題は、どうやって Γ あるいは G を測定するかである。 我々はまず、次式で与えられる全断面積を測定できる。
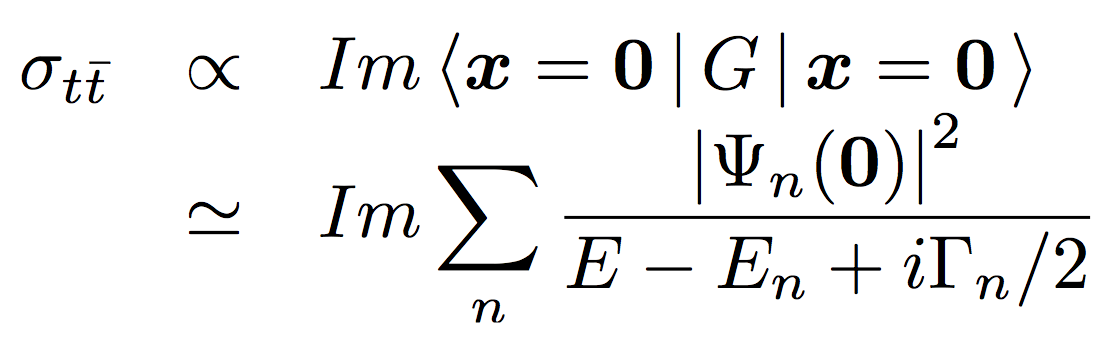
ここで、n の和は、全てのトップオニアム共鳴状態についてとる。 全断面積の測定は、波動関数の原点での値の絶対値のみに 依存することが分かる。
一方、微分断面積(トップの運動量分布)は、運動量空間での 波動関数の形を直接的に反映している。
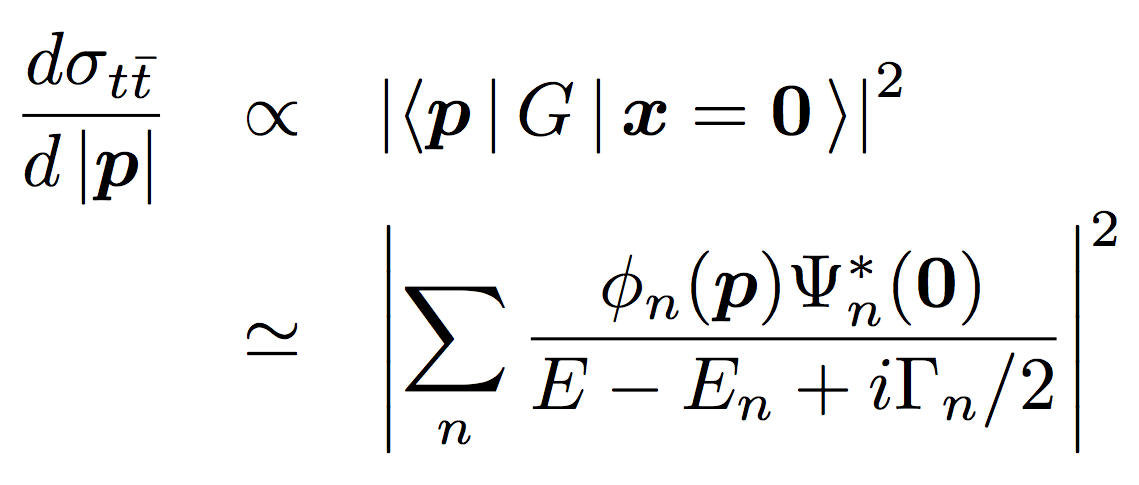
クォークオニアムの波動関数の測定はトップクォークに至って 初めて可能となる点は強調されて良い。 他の軽いクォークオニアムでは、崩壊が対消滅で起こるので、 クォークオニアム中のクォークや反クォークの運動量に関する情報は 失われてしまう。 トップの場合は、トップ崩壊の子供の粒子(b-クォーク、 W の崩壊で出来たクォーク・反クォーク対)の運動量の和として、 親のトップの運動量を測定することが出来る。
全断面積は、しきい値領域でエネルギー・スキャンを行うことで、トップの運動量分布は、トップの3ジェットへの崩壊を再構成することで測定出来る。