

Next: 軽いヒッグスが無かった場合
Up: 超対称性理論のシナリオ
Previous: ヒッグス粒子探索
超対称性理論の予言どうり軽いヒッグスが発見され、
ヒッグスセクターのノンミニマリティ(標準理論からのずれ)が確立されたとしても、
この理論を最終的に検証するためには, 超対称性粒子を発見しなければならない。
図-17a は、最も軽いチャージーノの質量が
理論のパラメータによりどう変化するかを示している。
図-17b はスレプトンとスクォークに対する同様な図である。
Figure 17:
超粒子の質量の等高線:(a) チャージーノ、(b)スレプトンとスクォーク
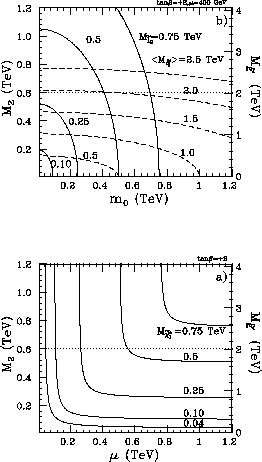 |
スクォーク、グルイーノといった強い相互作用をする超対称粒子の質量が、
スレプトンやチャージーノ等の強い相互作用をしない粒子より軽い点に注目したい。
強い相互作用をしない超対称粒子はハドロンコライダーでは、
発見が困難である。
一方、電子・陽電子反応では、
これらの粒子の対生成はしきい値ぎりぎりまで探索可能であり、
重心系エネルギー1 TeV のリニアコライダーは、
LHC 等のハドロンコライダーをしのぎ、
重心系エネルギー 500 GeV での JLC の初期実験でも、
LHC では探索不可能な部分を相補的に探索できることが分かる。
ひとたび、超対称粒子が発見されれば、後は リニアコライダーの
独壇場である。
i) 超対称粒子の研究
超対称粒子は通常の粒子と最も軽い超対称粒子(LSP)に崩壊する
(通常最も軽いニュートラリーノ 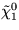 が LSP だと考えられている)。
この LSP は安定で物質とほとんど相互作用をしないため、
検出されない。
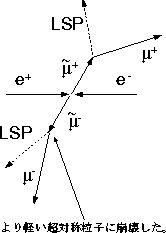
そこで、超対称粒子生成のシグナルは終状態に運動量欠損のある
折れ曲がった事象となる(図-18)。
が LSP だと考えられている)。
この LSP は安定で物質とほとんど相互作用をしないため、
検出されない。
そこで、超対称粒子生成のシグナルは終状態に運動量欠損のある
折れ曲がった事象となる(図-18)。
Figure 18:
超対称粒子生成事象の典型的な形
 |
そこで、超対称粒子探索のバックグラウンドとなるのは、
LSP と同様検出されないニュートリノを出す標準理論の反応である。
ここで威力を発揮するのが偏極電子ビームという
電子・陽電子リニアコライダーならではの強力な武器である。
図-19 は、ミュー粒子の超対称の相棒である
スカラーミューオンの対生成のアコプラナリティー角の分布を、
無偏極の電子ビームの場合(a)と偏極が +0.95 の場合(b)について示している。
Figure 19:
スカラーミューオン対生成のアコプラナリティー角の分布:
(a) 無偏極の電子ビームの場合、(b) 偏極が +0.95 の場合
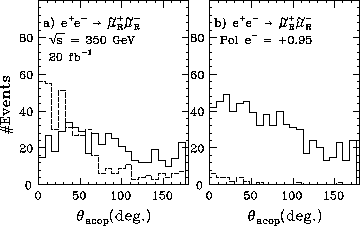 |
破線は W対生成のバックグラウンド、実線がシグナルである。
W 対生成は、SU(2)L のゲージボソンの関与する反応であるため、
W や Z の質量が無視できるようになる JLC のエネルギー領域では
対称性が回復し始め、
左巻き電子しか反応に関与できなくなる。
そのため右偏極の偏極ビームの使用で、バックグラウンドが大幅に落る。
一方、シグナルは、右巻き電子により強く結合するので
ほぼ倍増することが分かる。
つまり、2重に得するのである。
アコプラナリティー角を 30 度でカットすれば、
バックグラウンドはほぼ完全になくなる。
このサンプルを用いて超対称粒子の質量の精密測定が出来る。
測るべき量は、スカラーミューオンの崩壊から来る
ミュー粒子のエネルギー分布である(図-20a)。
この分布の上端と下端は、2体崩壊なので、
親であるスカラーミューオンの質量と崩壊で生じる LSP の質量で決まる。
Figure 20:
(a) スカラーミューオンの崩壊で生じたミュー粒子の
エネルギー分布、(b) フィットで決まる超粒子の質量
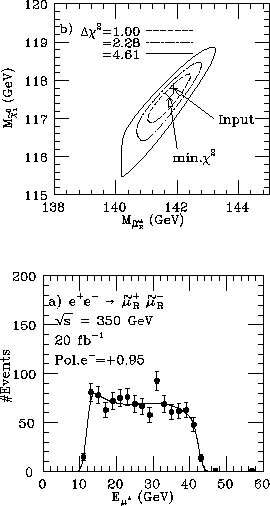 |
そこで、このエネルギー分布を
スカラーミューオンの質量と LSP の質量をパラメータとしてフィットすると、
図-20b のようにスカラーミューオンと
LSP( )の質量が 1% の精度で決まる。
)の質量が 1% の精度で決まる。
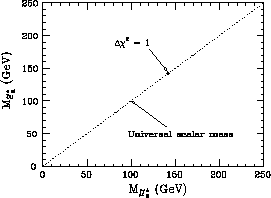
ii) プランクスケールの物理への展望
超対称性の破れ(通常粒子と対応する超粒子の質量差)は、
超対称性を破る超高エネルギーの物理で決まっていると期待される。
例えば、スカラー電子とスカラーミューオンの質量は、
超重力による超対称性の破れのシナリオでは、等しくなる。
そこで、これらの質量が測定されれば、プランクスケールに近い
超高エネルギーの物理のテストが出来ることになる
(図-21)。
Figure 21:
普遍スカラー質量の仮定の検証
 |
このように、ひとたび JLC で超対称性が発見されれば、
大統一、超重力といった超高エネルギーの物理を
調べる初めての現実的可能性が開けることになる。
JLC-I によるわずか 数 100 GeV のステップが
プランクスケールに迫る巨大なステップとなりうるわけである。
これは、恐るべき可能性である。


Next: 軽いヒッグスが無かった場合
Up: 超対称性理論のシナリオ
Previous: ヒッグス粒子探索
Keisuke Fujii
5/2/2000

![]() が LSP だと考えられている)。
この LSP は安定で物質とほとんど相互作用をしないため、
検出されない。
そこで、超対称粒子生成のシグナルは終状態に運動量欠損のある
折れ曲がった事象となる(図-18)。
が LSP だと考えられている)。
この LSP は安定で物質とほとんど相互作用をしないため、
検出されない。
そこで、超対称粒子生成のシグナルは終状態に運動量欠損のある
折れ曲がった事象となる(図-18)。