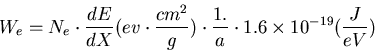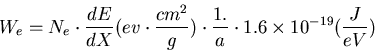Next: wakefield
Up: Collimation
Previous: collimation depth
When the beam hits on the collimator, the temperature grows up on the surface.
The energy deposit on the surface (J/g) can be expressed by,
| 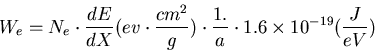 |
(1) |
where Ne particles hit on the surface area of a (cm2).
The thermal energy due to a temperature rise (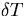 ) is given by,
) is given by,
| 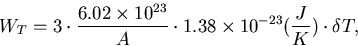 |
(2) |
where, A is an atomic mass number.
The temperature rise due to the energy deposit can be obtained by WT = We.
Apparently, a material with smaller atomic number is better for the collimator
if its melting temperature is high enough. The relevant properties of several
atoms are listed in table 1.
Carbon seems to be the best on this point. Is it true?
Table 1:
Candidate materials for collimator
| material |
A |
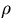 |
X0 |
Tmelt |
Tboil |
Tstress |
| |
|
g / cm3 |
cm |
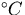 |
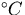 |
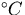 |
| C |
12 |
2.25 |
18.8 |
3700 |
4800 |
< 2500 |
| Ti |
47.9 |
4.51 |
3.56 |
1660 |
3277 |
< 1000 |
| W |
183.8 |
19.24 |
0.35 |
3410 |
5900 |
? |
| Cu |
63.5 |
8.93 |
1.43 |
1080 |
3000 |
< 180 |
| Fe |
55.8 |
7.87 |
1.76 |
1535 |
2750 |
? |




Next: wakefield
Up: Collimation
Previous: collimation depth
Toshiaki Tauchi
12/20/1999