




Next: Algorithm
Up: Breit-Wheeler Process
Previous: Formulas
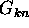 are 3-argument functions. In order to avoid discontinuities
due to the n-photon threshold, following variables (in addition to
are 3-argument functions. In order to avoid discontinuities
due to the n-photon threshold, following variables (in addition to 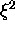 )
are used as the independent variables instead of (
)
are used as the independent variables instead of (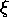 ,
, 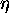 , x):
, x):
- q
- Defined by
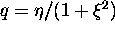 . The n-photon threshold is
given by
. The n-photon threshold is
given by 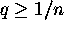 .
.
- y
- Defined by
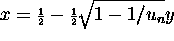 .
. 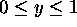 represents electrons with energy
represents electrons with energy 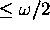 and
and
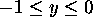 those
those 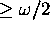 . Since
. Since 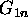 and
and 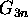 are even functions of y, only the part
are even functions of y, only the part
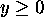 is tabulated.
is tabulated.
Now, the initialization is done by
C ALL NLBWST(MY,MPH,MXI,MQ,XIMAX,ETAMAX,LENHBW,ENHBWF,IRTN)
- MY
- Number of y's. (i-th y point is
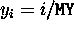 ,
,
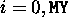 )
)
- MPH
- Maximum number of laser photons. (
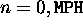 )
)
- MXI
- Number of
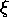 's. (
's. (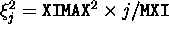 ,
,
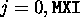 )
)
- MQ
- Number of q's. Non-equally-spaced MQ points are
selected in
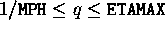 .
.
- XIMAX
- Maximum
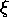 .
.
- ETAMAX
- Maximum
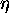 . Must satisfy
. Must satisfy 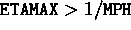 .
Otherwise, no pair creation is possible.
.
Otherwise, no pair creation is possible.
- LENHBW
- Flag to apply a rate enhancement function.
- ENHBWF
- Enhancement function name declared external. Used when
LENHCP
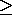 1.
1.
- IRTN
- Return code.
The parameters MY, MPH, MXI can be different from those
for nlcpst. A second call of NLBWST will replace the parameters
and the arrays created in the first call.
The enhancement function, if needed, has to be defined as
FUNCTION ENHBWF(Y)
REAL*8 ENHBWF,Y
ENHBWF=......
RETURN
END
The enhancement function has to be a function of
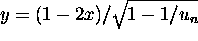 (
(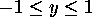 ) only and it
must be an even function of y and
) only and it
must be an even function of y and 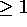 for all y. (Actually, only the part
for all y. (Actually, only the part
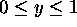 is used.)
The probability functions
is used.)
The probability functions 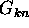 are multiplied
by ENHBWF(y). Note that
are multiplied
by ENHBWF(y). Note that 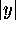 close to 1 represents events
with a large unbalance of energy between final electron and positron.
See NLBWGN for how the weight should be treated
in the simulation.
close to 1 represents events
with a large unbalance of energy between final electron and positron.
See NLBWGN for how the weight should be treated
in the simulation.
Possible errors
1ex
- IRTN=1000
- Memory insufficient. You have to reduce
MY
 MPH
MPH MXI
MXI MQ
or increase the parameter MW in the FORTRAN source.
MQ
or increase the parameter MW in the FORTRAN source.
- IRTN=1001 to 1004
- Either one of
MY,MPH,MXI,MQ is too large.
- IRTN=1100
- The enhancement function less than 1 at some y.
An event is generated by
1ex
NLBWGN(PG,HG,WL,NL,HL,PD,DT,PMAX,IRR,NPH,PELE,HELE,PPOS,HPOS,
PROB,WGT,IRTN)
Input variables
- PG
- Array of dimension (0:3).
Initial (high energy) photon 4-momentum (eV/c).
- HG
- Photon helicity. (
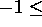 HG
HG 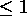 ).
).
- WL
- Laser photon energy (eV).
- NL
- Array of dimension 3. Unit vector along the laser direction.
- HL
- Laser helicity (-1 or +1).
- PD
- Laser power density (Watt/m
 ).
).
- DT
- Time interval times the velocity of light (meter).
- PMAX
- Maximum probability of pair creation in DT.
Same as in NLCPGN.
- IRR
- Random number seed.
Output variables
- NPH
- If
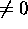 , number of absorbed laser photons.
If 0, no pair creation.
, number of absorbed laser photons.
If 0, no pair creation.
- PELE
- Array of dimension (0:3). 4-momentum of final electron.
- HELE
- Helicity of final electron.
- PPOS
- Array of dimension (0:3). 4-momentum of final positron.
- HPOS
- Helicity of final positron.
- PROB
- Calculated event probability. Same as in NLCPGN.
- WGT
- Event weight. Same as in NLCPGN.
- IRTN
- Return code.
The event weight is always 1 if initialized with LENHBW=0.
When WGT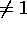 (actually,
(actually, 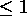 ), each of the final pair should be
asigned the weight
), each of the final pair should be
asigned the weight 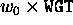 and the initial photon still be retained
with the weight
and the initial photon still be retained
with the weight 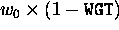 , where
, where 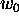 is the weight of the
initial photon before the event. When WGT=1, the initial photon
should be eliminated.
is the weight of the
initial photon before the event. When WGT=1, the initial photon
should be eliminated.
Possible errors
- IRTN=1000
- Initialization nit yet done.
- IRTN=1001
-
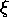 is larger than XIMAX.
is larger than XIMAX.
- IRTN=1002
-
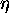 is larger than ETAMAX.
is larger than ETAMAX.
- IRTN=100
- The total rate exceeds PMAX.
Real*8 function
N LBWFN(KK,K,NPH,XI,ETA,X)
returns the value of the function 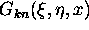 ,
where k=K, n=NPH,
,
where k=K, n=NPH, 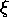 =XI,
=XI, 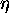 =ETA,
and x=X=
=ETA,
and x=X=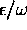 .
The first argument KK selects either the direct calculation
using a Bessel function routine (KK=1) or use interpolation of the
stored table (KK=2).
In the latter case, initialization must be done in advance
and K must be 1 or 3.
.
The first argument KK selects either the direct calculation
using a Bessel function routine (KK=1) or use interpolation of the
stored table (KK=2).
In the latter case, initialization must be done in advance
and K must be 1 or 3.





Next: Algorithm
Up: Breit-Wheeler Process
Previous: Formulas
Toshiaki Tauchi
Thu Dec 3 17:27:26 JST 1998
![]() are 3-argument functions. In order to avoid discontinuities
due to the n-photon threshold, following variables (in addition to
are 3-argument functions. In order to avoid discontinuities
due to the n-photon threshold, following variables (in addition to ![]() )
are used as the independent variables instead of (
)
are used as the independent variables instead of (![]() ,
, ![]() , x):
, x):
![]() ,
where k=K, n=NPH,
,
where k=K, n=NPH, ![]() =XI,
=XI, ![]() =ETA,
and x=X=
=ETA,
and x=X=![]() .
The first argument KK selects either the direct calculation
using a Bessel function routine (KK=1) or use interpolation of the
stored table (KK=2).
In the latter case, initialization must be done in advance
and K must be 1 or 3.
.
The first argument KK selects either the direct calculation
using a Bessel function routine (KK=1) or use interpolation of the
stored table (KK=2).
In the latter case, initialization must be done in advance
and K must be 1 or 3.